Предмет: Алгебра,
автор: bertain
100 б + лучший ответ! Исследовать на непрерывность (с подробным решением);
Приложения:
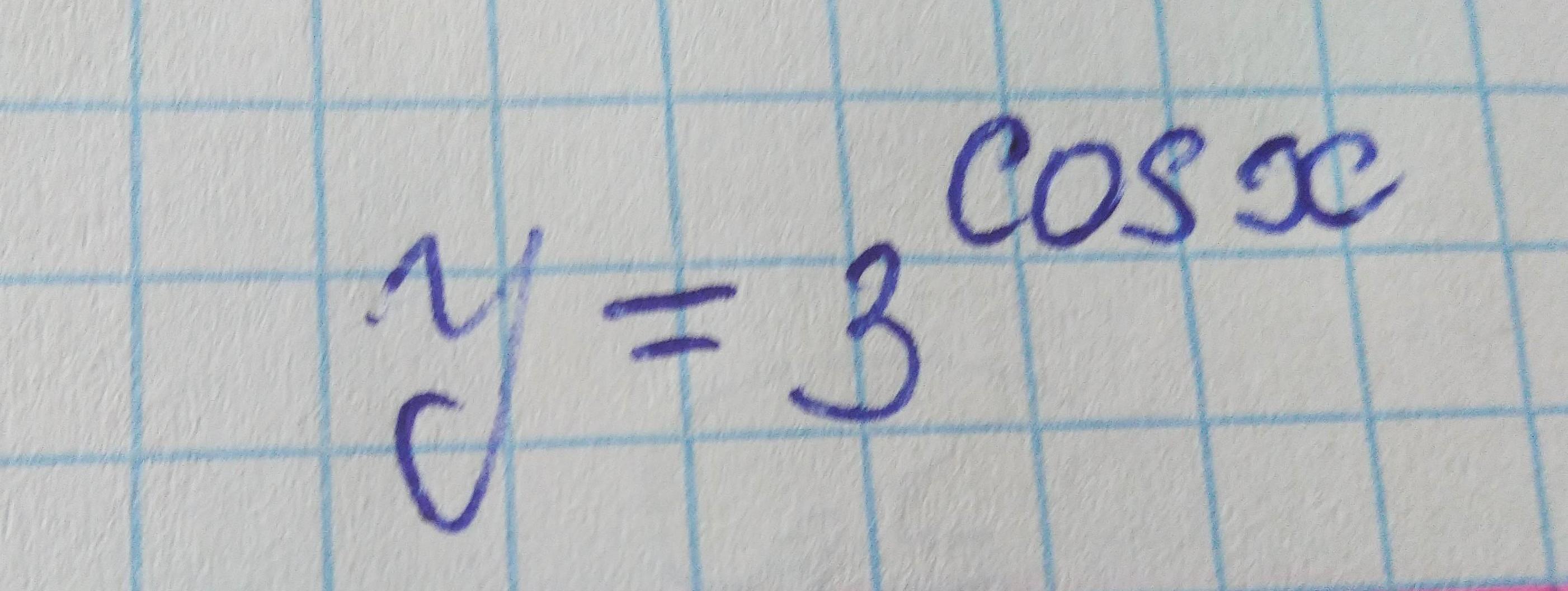
Ответы
Автор ответа:
1
Ответ: функция непрерывна на всей числовой оси.
Объяснение:
Функция cos(x), а вместе с ней и функция y=3^[cos(x)], определена на всей числовой оси. Мы докажем непрерывность функции в точке x0, где x0 - любая точка числовой оси, если докажем стремление к нулю выражения y(x0+Δx)-y(x0) при Δx⇒0. Но y(x0+Δx)-y(x0)=3^cos(x0+Δx)-3^cos(x0)=3^[cos(x0)*cos(Δx)-sin(x0)*sin(Δx)]-3^cos(x0). При Δx⇒0 cos(Δx)⇒1, а sin(Δx)⇒0, поэтому выражение cos(x0)*cos(Δx)-sin(x0)*sin(Δx) стремится к cos(x0), а выражение 3^[cos(x0)*cos(Δx)-sin(x0)*sin(Δx)]-3^cos(x0) - к нулю. Таким образом доказана непрерывность данной функции на всей числовой оси.
Интересные вопросы
Предмет: Математика,
автор: emiliyaseed
Предмет: Математика,
автор: usernameee52
Предмет: География,
автор: hahahahate
Предмет: История,
автор: TANKIST20051
Предмет: Математика,
автор: chehol8akakto