Предмет: Алгебра, автор: noname09011

Логарифмическое неравенство

Приложения:

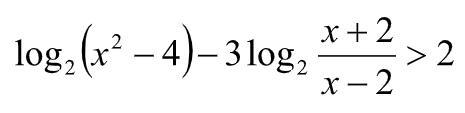
Ответы

Автор ответа: hote

$\displaystyle log_2(x^2-4)-3log_2\frac{x+2}{x-2}>2\\\\ODZ:\\\\\left \{ {{x^2-4>0} \atop {\frac{x+2}{x-2}>0; x-2\neq 0 }} \right. \\\\(-oo;-2) (2;+oo)$

при х>2 (х+2)>0; (x-2)>0 тогда

$\displaystyle log_2(x-2)(x+2)-3(log_2(x+2)-log_2(x-2))>2\\\\log_2(x-2)+log_2(x+2)-3log_2(x+2)+3log_2(x-2)>2\\\\4log_2(x-2)-2log_2(x+2)>2\\\\2(2log_2(x-2)-log_2(x+2)>2\\\\log_2(x-2)^2-log_2(x+2)>1\\\\log_2\frac{(x-2)^2}{x+2}>1$

$\displaystyle \frac{(x-2)^2}{(x+2)}>2^1\\\\\frac{(x-2)^2-2(x+2)}{x+2}>0\\\\\frac{x^2-6x}{x+2}>0\\\\\frac{x(x-6)}{x+2}>0$

__-____-2___+___0__-___6__+___

ответом на неравенство будет промежуток (-2;0)∪(6;+∞)

с учетом условия (6;+∞)

при х<-2 (x+2)<0; (x-2)<0 тогда

$log_2(-x+2)+log_2(-x-2)-3log_2(-x-2)+3log_2(-x+2)>2\\\\4log_2(2-x)-2log_2(-x-2)>2\\\\2(2log_2(2-x)-log_2(-x-2)>2\\\\log_2(2-x)^2-log_2(-x-2)>1\\\\log_2\frac{(2-x)^2}{(-x-2)}>1\\\\\frac{(2-x)^2}{(-x-2)}>2^1\\\\\frac{(2-x)^2-2(-x-2)}{x+2}>0\\\\\frac{x^2-2x+8}{-(x+2)}>0$