Предмет: Алгебра,
автор: dasamakiseva
Нужно найти производную функции
Приложения:
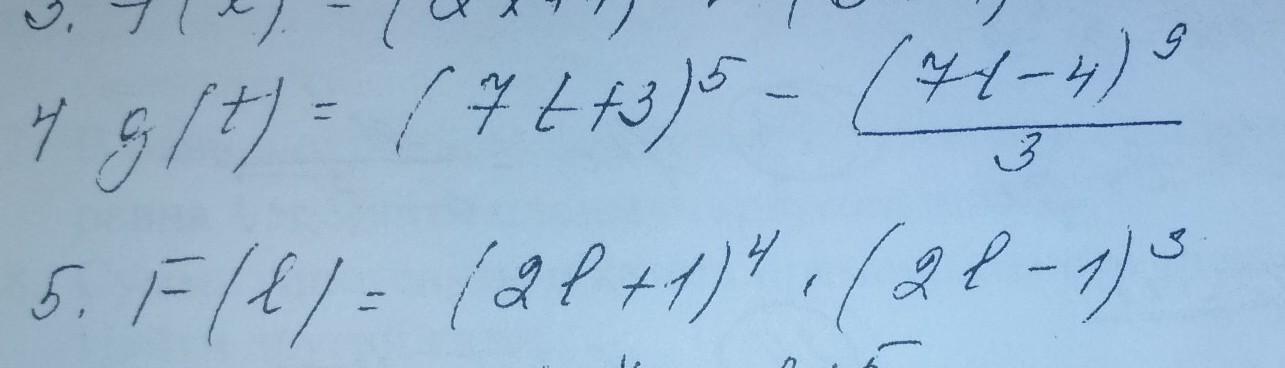
Ответы
Автор ответа:
1
Автор ответа:
1
Ответ:
Объяснение:
4)g(t)'=((7t+3)^5 - ((7t-4)^9)/3)'=(7t+3)^5'-1/3*(7t-4)^9)'=5*(7t+3)^4*(7t+3)'-1/3*9*(7t-4)^8)*(7t-4)'=5*(7t+3)^4*7-3*(7t-4)^8)*7=35*(7t+3)^4-21*(7t-4)^8)*7
F(l)'=(2l+1)^4×((2l-1)^3=((2l+1)^4)'×(2l-1)^3+(2l+1)^4×((2l-1)^3)'=4×(2l+1)^3×2×(2l-1)^3+(2l+1)^4×3×((2l-1)^2)×2=8((2l-1)×(2l-1))^3+6((2l+1)^2×(2l+1)^2)×(2l+1)^2=8(4l^2-1)^2+6((2l+1)^2×(4l^2-1)^2;
Интересные вопросы
Предмет: Українська мова,
автор: angelinahritsak
Предмет: Литература,
автор: sofiaantipuk
Предмет: Химия,
автор: qadawratral
Предмет: Информатика,
автор: Алкадиеныч