Предмет: Математика,
автор: vajslav
4 номер по планиметрии 100б
Приложения:
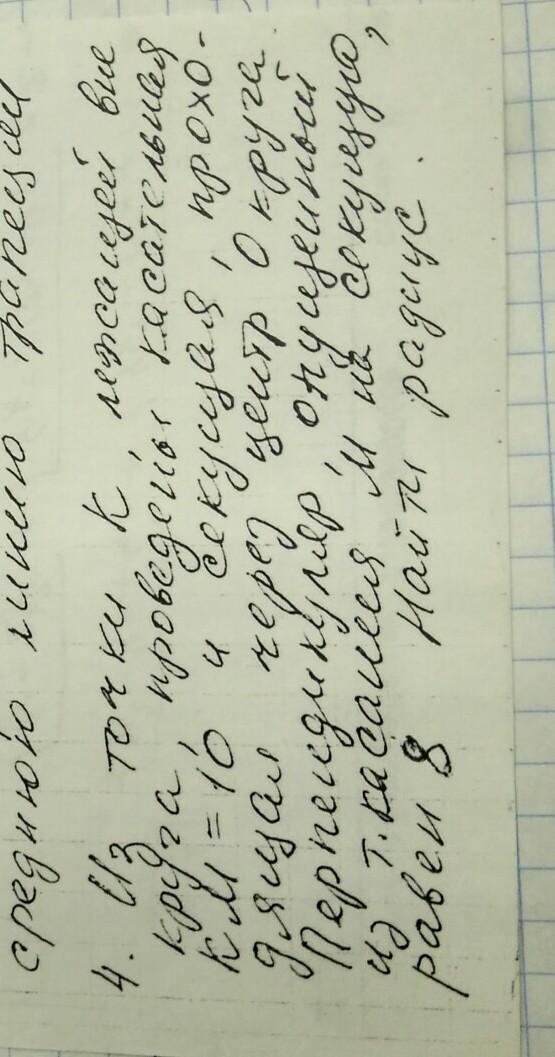
Ответы
Автор ответа:
4
Ответ:
.
Пошаговое объяснение:
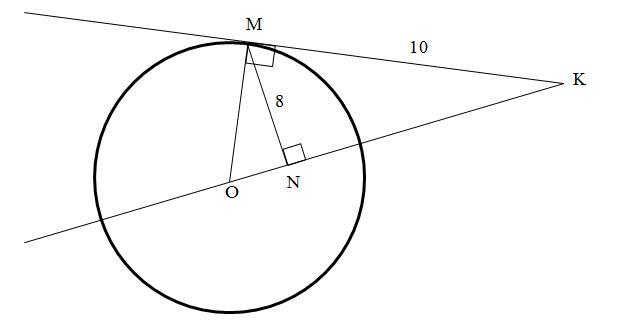
Дано (см. рисунок):
KM - касательная к окружности
KO - секущая окружности
KM=10
MN=8
∠MNK=90°
Найти радиус r.
Решение.
Известно, что радиус окружности перпендикулярен к касательной в точке касания M, то есть ∠OMK=90°.
Рассмотрим треугольники Δ MNK и ΔMOK:
∠MKN=∠MKO, ∠MNK=∠OMK=90° и в силу свойства о подобии треугольников треугольники Δ MNK и ΔMOK подобны. Тогда
или
или
r=10·8/KN=80/KN.
Но Δ MNK прямоугольная и поэтому для него верна теорема Пифагора:
MK²=MN²+KN² или KN²=MK²-MN²=10²-8²=100-64=36=6² или KN=6.
r=80/KN=80/6=40/3.
Ответ: .
Приложения:
Интересные вопросы
Предмет: Математика,
автор: Animeshnik0160
Предмет: Химия,
автор: skalamiec
Предмет: Математика,
автор: ivanivnag92
Предмет: Математика,
автор: armovi
Предмет: Биология,
автор: Angela073