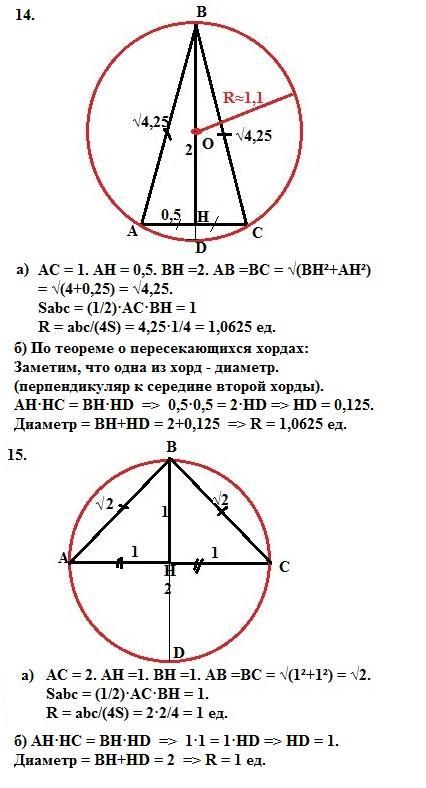
14) найдите радиус окружности, описанной около равнобедренного треугольника, основание которого равно 1, а высота равна 2. Изобразите эту окружность.

15)найдите радиус окружности, описанной около равнобедренного треугольника, основание которого равно 2, а высота равна 1. Изобразите эту окружность. решите пожалуйста, даю 50 баллов!!!! ​

Ответ:

14. R = 1,0625 ед. 15. R = 1 ед.

Вариант 2. 15 R = R = 2√3/3 ед.

Объяснение:

Вариант1. Высота проведена к основанию.

14.  АС = 1. АН = 0,5. ВН =2. АВ =ВС = √(ВН²+АН²) = √(4+0,25) = √4,25.

Sabc = (1/2)·AC·BH = (1/2)·1·2 = 1

R = abc/(4S) = 4,25·1/4 = 1,0625 ед.

15. АС = 2. АН =1. ВН =1. АВ =ВС = √(1²+1²) = √2.

Sabc = (1/2)·AC·BH = (1/2)·2·1 =1.

R = abc/(4S) = 2·2/4 = 1 ед.

Или так: По теореме о пересекающихся хордах:

Заметим, что одна из хорд - диаметр (перпендикуляр к середине второй хорды).

14. АН·НС = ВН·HD  =>  0,5·0,5 = 2·HD => HD = 0,125.

Диаметр = ВН+HD = 2+0,125  => R = 1,0625 ед.

15. АН·НС = ВН·HD  =>  1·1 = 1·HD => HD = 1.

Диаметр = ВН+HD = 2  => R = 1 ед.

Вариант2. Высота проведена к боковой стороне.

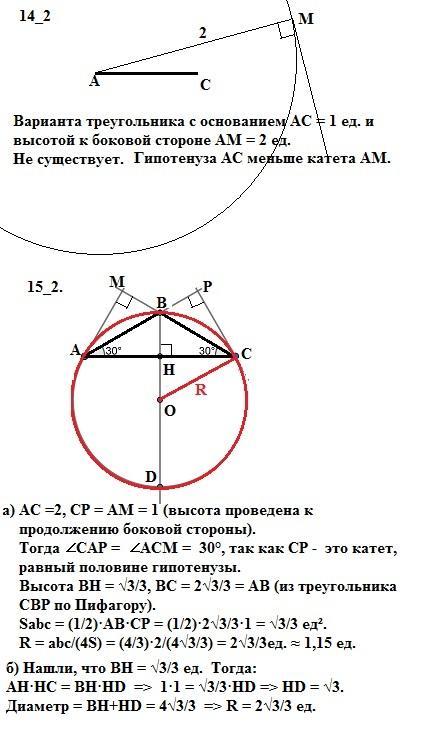
14_2. Не существует, так как высота - катет - больше основания (гипотенуза).

15_2.

а) АС =2, СР = АМ = 1 (высота проведена к продолжению боковой стороны).

Тогда ∠САР =  ∠АСМ =  30°, так как СР -  это катет, равный половине гипотенузы.  

Высота ВН = √3/3, ВС = 2√3/3 = АВ (из треугольника СВР по Пифагору).

Sabc = (1/2)·AВ·СР = (1/2)·2√3/3·1 = √3/3 ед².

R = abc/(4S) = (4/3)·2/(4√3/3) = 2√3/3ед. ≈ 1,15 ед.

б) Нашли, что ВН = √3/3 ед.  Тогда:

АН·НС = ВН·HD  =>  1·1 = √3/3·HD => HD = √3.

Диаметр = ВН+HD = 4√3/3  => R = 2√3/3 ед. ≈ 1,15 ед.