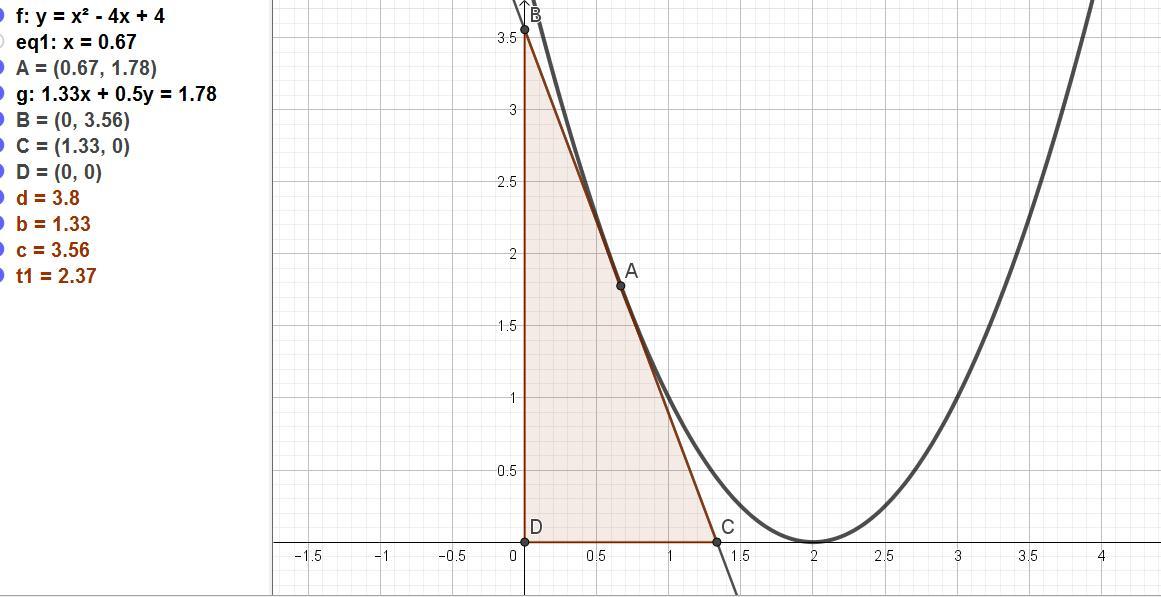
в каких точках надо провести касательные к графику функции y=(x-2)^2 ,что бы получить площадь треугольника ,ограниченного этой касательной и положительными полуосями координат,была наибольшией?

Такая точка одна. Находится как точка минимума функции площади заданного треугольника. Обозначим эту точку xо.

Уравнение касательной: y = y(xo)'(x - xo) + y(xo).

Функция x² - 4x + 4.

Производная в точке касания  равна y(xo)' = 2хo - 4.

Подставим: у = (2xo - 4)*(x - xo) + y(xo) =  (2xo - 4)*(x - xo) + (x - 2)² =

                   = 2xox - 4x - 2xo²+ 4xo + xo² - 4xo  + 4 =

                   = 2xox - 4x - 2xo² + xo² + 4 = 2xox - 4x - xo² + 4 =

                   = (2(xo - 2))x - xo² + 4.

В точке пересечения касательной с осью Оу переменная х = 0.

Тогда координата на оси Оу равна: у = - xo² + 4 = (2 - xo)(2 + хо).

В точке пересечения касательной оси Ох у равен 0:

0 = (2(xo - 2))x - xo² + 4.  

Отсюда х = (xo² - 4)/(2(xo - 2)) = ((xo - 2)(xo + 2)/(2(xo - 2)) = (xo + 2)/2.

Площадь треугольника равна:

S = (1/2)xy = (1/2)*((xo - 2)/2)*(4 - xo²) = (1/4)*(4xo + 8 - xo^3 - 2xo^2) =

  = (-1/4)xo^3 - (1/2)xo^2 + xo + 2.

Производную полученной функции приравниваем нулю.

(-3/4)xo^2 - xo + 1 = 0.

D=(-1)^2-4*(-0.75)*1=1-4*(-0.75)=1-(-4*0.75)=1-(-3)=1+3=4;

x_1=(2root4-(-1))/(2*(-0.75))=(2-(-1))/(2*(-0.75))=(2+1)/(2*(-0.75))=3/(2*(-0.75))=3/(-2*0.75)=3/(-1.5)=-3/1.5=-2 ( отрицательное значение отбрасываем).

x_2=(-2root4-(-1))/(2*(-0.75))=(-2-(-1))/(2*(-0.75))=(-2+1)/(2*(-0.75))=-1/(2*(-0.75))=-1/(-2*0.75)=-1/(-1.5)=-(-1/1.5)=-(-(2//3) )=2/3 ≈ 0.6667.

Ответ: х = (2/3), у = ((2/3) - 2)² = (-4/3)² = 16/9 ≈ 1,78.