Предмет: Алгебра, автор: Pqex

Срочно!!! 50 баллов!!!

Приложения:

ArtemCoolAc: А какой вариант и что конкретно?

Ответы

Автор ответа: ArtemCoolAc

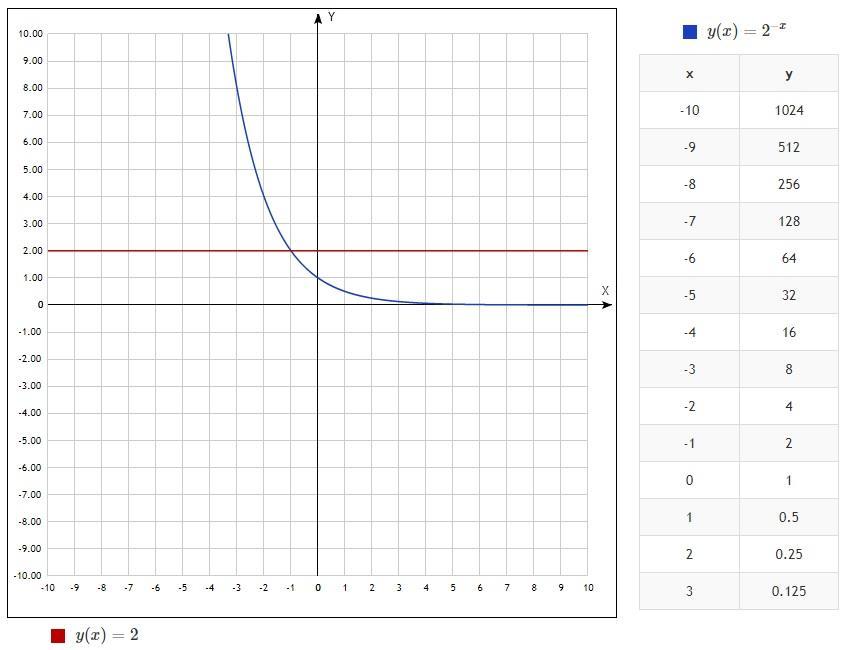
Построим график $\displaystyle y=\left(\frac{1}{2}\right)^x=(2^{-1})^x=2^{-x}$ , график показательной функции с убывающим показателем степени, достаточно стандартный, это слева. А справа просто прямая $y=2$

У нас неравенство $2^{-x} \leq 2$ , то есть прямая должна быть не ниже показательной функции, а это мы наблюдаем на промежутке

$x\in [-1;+\infty)$

Ответ: $\boxed{[-1;+\infty)}$

Теперь решаем из Б1 4 примера (так как обведено левое, я так понимаю, решаем именно с левой стороны):

а) $\displaystyle (1.5)^{\frac{x^2+x-20}{x}} \leq 1 \Rightarrow (1.5)^{\frac{x^2+x-20}{x}} \leq 1.5^0$

Так как $y=1.5^x$ - возрастающая функция, то есть при

$x_2>x_1: \ 1.5^{x_2}>1.5^{x_1}$ , то можем убирать основания и не менять знак неравенства:

$\displaystyle \frac{x^2+x-20}{x}\leq 0$

Разложим числитель на множители, для этого решим квадратное уравнение и найдем корни трехчлена:

$\displaystyle x^2+x-20=0; \ D=1^2-4\cdot 1\cdot (-20)=81=9^2; x=\frac{-1\pm9}{2} \\ x_1=-5; x_2=4\Rightarrow x^2+x-20=(x+5)(x-4)$

$\displaystyle \frac{(x+5)(x-4)}{x}\leq 0$

Нули функции известны, расставляем промежутки, знаки и получаем, что $x\in (-\infty; -5]\cup(0;4]$

Ответ: $\boxed{ (-\infty; -5]\cup(0;4]}$

б) $\displaystyle \left(\frac{1}{3}\right)^{x^2-4x-1} > 9^{x-1} \Rightarrow 3^{-x^2+4x+1}>3^{2x-2} \Rightarrow -x^2+4x+1>2x-2 \Rightarrow \\ x^2-2x-3>0 \Rightarrow x^2-2x+1-4>0 \Rightarrow (x-1)^2-2^2>0 \Rightarrow \\ \Rightarrow (x-1-2)(x-1+2)>0 \Rightarrow (x-3)(x+1)>0 \Rightarrow \\ \Rightarrow x\in(-\infty;-1)\cup(3;+\infty)$

Рассуждения аналогичные, как в пункте а) $y=3^x$ - возрастающая функция.

Ответ: $\boxed{(-\infty;-1)\cup(3;+\infty)}$

в) $\displaystyle 3^{x^2+1}-\left(\frac{1}{3}\right)^{-x^2}>162 \Rightarrow 3\cdot 3^{x^2}-3^{x^2}>2\cdot 81 \Rightarrow 2\cdot 3^{x^2}>2\cdot 3^4 \Rightarrow \\ \Rightarrow 3^{x^2}>3^4 \Rightarrow x^2>4 \Rightarrow x\in(-\infty;-2)\cup(2;+\infty)$

Рассуждения аналогичные, $y=3^x$ - возрастающая функция

Ответ: $\boxed{(-\infty;-2)\cup(2;+\infty)}$

г) $\displaystyle 5^x+5^{1-x}\geq 6 \Rightarrow 5^x+5\cdot\frac{1}{5^x}-6\geq 0; t=5^x, t>0\Rightarrow t+\frac{5}{t}-6\geq 0 \Rightarrow \\ \Rightarrow \frac{t^2-6t+5}{t}\geq 0\Rightarrow \frac{t^2-6t+9-4}{t}\geq 0 \Rightarrow \frac{(t-3)-2^2}{t}\geq 0 \Rightarrow \\ \Rightarrow \frac{(t-3-2)(t-3+2)}{t}\geq 0 \Rightarrow \frac{(t-5)(t-1)}{t}\geq 0 \ \bigg|\cdot t>0 \Rightarrow \\ \Rightarrow (t-5)(t-1)\geq 0 \Rightarrow \left [ {{t\geq 5} \atop {t\leq 1}} \right. \Rightarrow$

$\displaystyle \left [ {{5^x\geq 5^1} \atop {5^x \leq 5^0}} \right. \Rightarrow \left [ {{x\geq 1} \atop {x\leq 0}} \right. \Rightarrow x\in(-\infty;0]\cup[1;+\infty)$

Логика аналогичная, только здесь в принципе t в знаменателе так долго можно было не тащить, а сразу умножить на t>0 и не менять знак неравенства; $y=5^x$ - возрастающая функция

Ответ: $\boxed{(-\infty;0]\cup[1;+\infty)}$

Приложения:

Pqex: Господи, спасибо, милый человек!

ArtemCoolAc: В решении я не мог нормально прописать, там когда переходим уже к промежуткам, надо бы интервалы расставлять со знаками, надеюсь, умеете это делать. Из ответа ясно что где)