Предмет: Геометрия, автор: Аноним

срочно помогите!
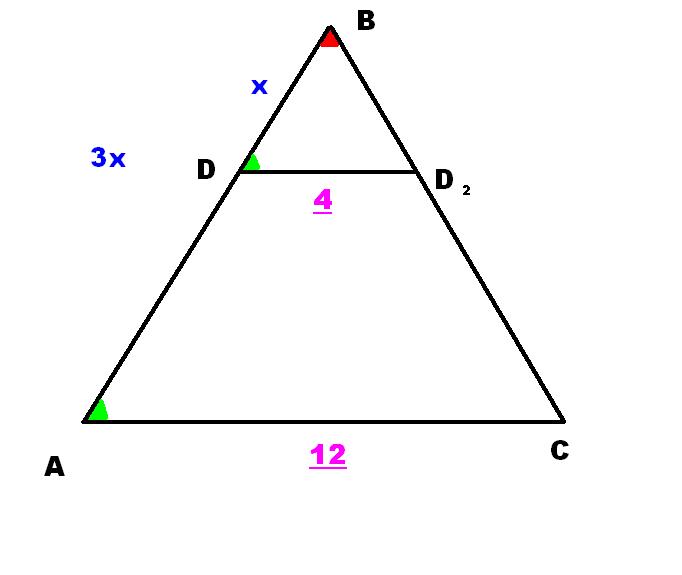
в треугольнике авс на стороне ав выбрана точка д такая, что вд:ва=1:3.
плоскость параллельна прямой ас, проходящей через д, пересекает отрезок вс в точке д2.
докажите что треугольнике двд2 подобен треугольнику авс .найдите ас если дд2=4 см.Пожалуйста мне очень нужна ваша помощь, пишите подробно!!!!

Ответы

Автор ответа: Artem112

Так как плоскость параллельна АС, то DD2||AC. Значит треугольники DBD2 подобен треугольнику АВС по двум углам (угол В - общий, угол ВDD2=угол ВАС как соответственные при пересечении двух параллельных прямых)
Находим коэффициент подобия этих треугольников: BD:BA=1:3 (он кстати дан)
Значит, DD2:AC=1:3
AC=DD2*3
AC=4cм*3=12см
Ответ: 12см

Приложения:

Автор ответа: Аноним

спасибо большое, а то я сегодня совсем ничего не соображаю, над простым задание сижу туплю)))

Автор ответа: emerald0101

Если плоскость проходит через прямую параллельную другой плоскости, то линия пересечения плоскостей параллельна данной прямой.
Т к плоскость, проходящая через D параллельна прямой AC, то линия пересечения данной плоскости с плоскостью треугольника АВС параллельна АС, т е $DD_2 parallel AC$ , следовательно треугольники $DBD_2$ и $ABC$ подобны с коэффициентом подобия $frac{1}{3}$ , т к по условию BD:BA=1:3. Тогда $DD_2:AC=1:3;AC=3DD_2=3*4=12.$