Предмет: Алгебра, автор: vokah71603

Пожалуйста, помогите

Приложения:

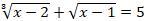
Ответы

Автор ответа: Universalka

0

$\sqrt[3]{x-2}+\sqrt{x-1}=5\\\\\sqrt[3]{x-2}=m,\Rightarrow x-2=m^{3},\Rightarrow x=m^{3}+2\\\\\sqrt{x-1}=n,\Rightarrow x-1=n^{2},\Rightarrow x=n^{2}+1\\\\\left \{ {{m+n=5} \atop {m^{3}+2=n^{2}+1}} \right. \\\\\left \{ {{n=5-m} \atop {m^{3}+2=(5-m)^{2}+1}} \right.\\\\\left \{ {{n=5-m} \atop {m^{3}+2=25-10m+m^{2}+1}} \right.\\\\\left \{ {{n=5-m} \atop {m^{3}-m^{2}+10m-24=0 }} \right.$

m³ - m² + 10m - 24 = 0

(m - 2)(m² + m + 12) = 0

1) m - 2 = 0

m = 2

2) m² + m + 12 = 0

D < 0 - корней нет

x - 2 = m³

x - 2 = 2³

x - 2 = 8

x = 10

Ответ : 10

mabilacom: Здравствуйте. Помогите с заданием.
https://znanija.com/task/33639782?utm_source=android&utm_medium=share&utm_campaign=question

Автор ответа: Аноним

0

Если переписать это уравнение как

∛(х-2)=5-√(х-1), то видно, что правая часть у=5-√(х-1) убывающая при х ∈[1;+∞], а функция у=∛(х-2) возрастающая при х ∈(-∞;+∞)

Значит, если есть корень у этого уравнения, то он единственный. И легко угадываемый. х=10

Ответ х=10

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Математика, автор: antoninatoto34

через образующие угол между которыми 120 градусов проведена плоскость составляющая с основанием угол 45° Найдите объём конуса если его высота равна корень из 6

5 лет назад

Предмет: Алгебра, автор: frunz4525

Найдите главный абзац этой функции

5 лет назад

Предмет: Русский язык, автор: ghfgcvcvcc46

упражнение 5 помогиите пожалуста ответ

5 лет назад

Предмет: Математика, автор: nytexx

-х=35, х=??
Ребенок доказывает, что в школе учат, что х=35, не -35. Почему??

9 лет назад

Предмет: Математика, автор: Энверик

используя линии квадратной сетки тетради , постройте углы, равные 45 градусов и 135 градусов

9 лет назад