Предмет: Математика, автор: xxxnastyaxxx1991

решите интеграл. нужно подробное расписание примеров

Приложения:

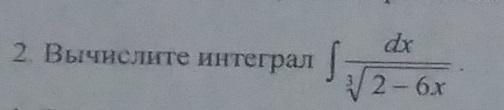
Ответы

Автор ответа: dmasya

0

Ответ:

Пошаговое объяснение:

-1/6∫(d(2-6x))/∛(2-6x)=-1/6∫(2-6x)^(-1/3)=-1/4*(2-6x)^(2/3)

Автор ответа: axatar

2

Ответ:

$\int\limits {\frac{1}{\sqrt[3]{2-6x} } } \, dx=\int\limits {(2-6x)^{-\frac{1}{3} } } \, dx= -\frac{1}{6} \int\limits {(2-6x)^{-\frac{1}{3} } } \, d(2-6x)=\\=-\frac{1}{6} *\frac{(2-6x)^{-\frac{1}{3}+1 }}{-\frac{1}{3}+1 } +C=-\frac{1}{6} *\frac{(2-6x)^{\frac{2}{3}}}{\frac{2}{3} } +C=-\frac{1}{6} *\frac{3}{2} *(2-6x)^{\frac{2}{3}}+C=\\=-\frac{1}{4} \sqrt[3]{(2-6x)^{2} }+C$

Аноним: Нет константы + С

axatar: Да, Я забыл константу добавить! Спасибо!

axatar: И уже исправил!

Аноним: :)

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: xiaotopchik9

ПОМОГИТЕ ПЖ СРОЧНО!! ЖЕЛАТЕЛЬНО С ОБЪЯСНЕНИЕМ
1. Дайте определения таким терминам, как глагол и неопределённая форма глагола. 2. Прочитайте слова и определите их начальную форму: ходила, думал, играли, извлекал, мылась, приготовила. 3. Выучите семнадцать глаголов на -ять и один на ить и запомните их правописание.

2 года назад

Предмет: Алгебра, автор: zamistitelv

Две бригады могут проделать всю работу, работая вместе, за 18 дней. Если
первая бригада будет работать сама 9 дней, а впоследствии приступит к работе вторая, то
для окончания работы им нужно еще 12 дней. За сколько дней выполнит работу первая
бригада, работая самостоятельно?

2 года назад

Предмет: Русский язык, автор: xiaotopchik9

СРОЧНО!
В каком ряду слов допущена ошибка? Сеять, хаять, надеяться, блеять Таять, веять, клеить, замеять, кланяться Реять, баять, чаять, маяться, лелеять Чуять, каяться, лелеить, кашлять, лаять

2 года назад

Предмет: Биология, автор: polihka20

таблица сравнения сперматогенеза и овогенеза! помогите, для зачета! пожалуйста срочно!

9 лет назад

Предмет: Физика, автор: mixa867

решите срочно!!!!!!!!!!! !

9 лет назад