Предмет: Геометрия,
автор: lololoshka6143
док ва..............
Приложения:
Simba2017:
чего доказывать то?
что они паралельные
Ответы
Автор ответа:
4
Ответ:
Доказано!
Объяснение:
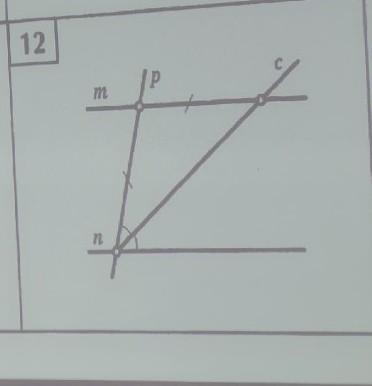
Дано:
Δ ABC;
AB = BC; ∠ 1 = ∠ 2.
m и n - прямые, пересекающиеся с помощью секущих c и p.
Доказать:
m || n (автор вопроса указал в комментариях)
Доказательство:
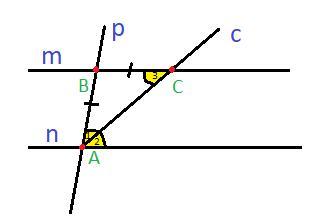
Δ ABC - равнобедренный (т.к. боковые стороны, т.е. AB и BC равны) ⇒ по свойству равнобедренного тр-ка (углы при основании в равнобедренном тр-ке равны) ∠ 1 = ∠ 3.
Т.к. ∠ 1 = ∠ 3 и ∠ 1 = ∠ 2, то ∠ 2 = ∠ 3, а они накрест лежащие при прямых m и n и секущей с ⇒ m || n (по теореме: если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны)
Доказано!
Приложения:
Интересные вопросы
Предмет: Українська мова,
автор: egorgolovchenko1995
Предмет: Математика,
автор: eva2112eva
Предмет: Математика,
автор: baharchike
Предмет: Физика,
автор: Logikmaster
Предмет: Алгебра,
автор: furyAwake