Предмет: Геометрия, автор: vadzxc

Прошу помогите 1 задание завтра контрольная работа)))) Если сделаете огромное спасибо!
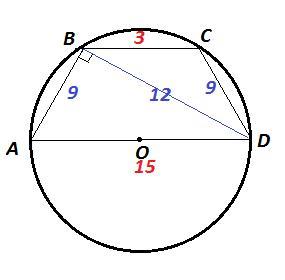
Трапеция ABCD вписана в окружность(рис.3), центр О которой лежит на большем основании AD. Найдите радиус вписанной окружности, если CD=9 см, BD=12 см.

Приложения:

Ответы

Автор ответа: xERISx

Дано: трапеция ABCD вписана в окружность с центром в т. О,

AD║BC, O∈AD, CD=9 см, BD=12 см

Найти: r - ?

Решение:

В окружность можно вписать только равнобедренную трапецию

⇒ AB = CD = 9 см

ΔABD вписан в окружность по диаметру

⇒ ΔABD - прямоугольный. Теорема Пифагора

$AD^2=AB^2+BD^2=9^2+12^2=225=15^2$

AD = 15 см

Вписать окружность можно только в тот четырёхугольник, у которого суммы противоположных сторон равны

BC+AD = AB+CD ⇒ BC = AB+CD-AD=9+9-15 = 3 см

ΔBCD : CD=9 см; BC=3 см; BD=12 см

3 + 9 = 12 - ΔBCD не может существовать, так как для него не выполняется неравенство треугольника: сумма двух сторон треугольника должна быть БОЛЬШЕ третьей стороны.

Следовательно, нет возможности выполнить условие для вписанной окружности, т. е. в данную трапецию вписать окружность НЕЛЬЗЯ.

Приложения: