Срочно пжпжпжпжп все три номера

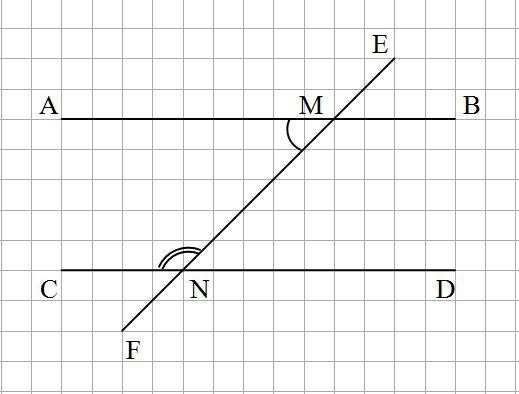
1). (Рис.1)  ∠CNM = 3∠AMN

    Так как  ∠CNM и ∠AMN - внутренние односторонние при

    параллельных и секущей, то:

    ∠CNM + ∠AMN = 180°

    4∠AMN = 180

      ∠AMN = 45°     ∠CNM = 135°

∠AMN = ∠MND = 45°, а также ∠BMN = ∠CNM = 135°, как внутренние накрест лежащие.

∠AMN = ∠EMB = 45°;  ∠AME = ∠BMN = 135°, как вертикальные

∠AME = ∠FND = 135°, а также ∠BME = ∠CNF = 45°, как внешние накрест лежащие.

Таким образом:

∠AME = ∠FND = ∠BMN = ∠CNM = 135°

∠BME = ∠CNF = ∠AMN = ∠MND = 45°

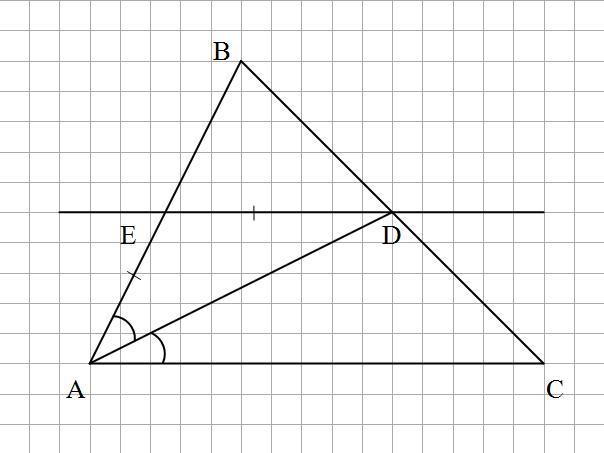
2. (Рис.2)  Так как ∠ВАС = 68°  и  AD - биссектриса, то:

                    ∠EAD = ∠DAC = 68 : 2 = 34°

                 Так как AE = ED, то   ΔAED - равнобедренный и

                     ∠EAD = ∠EDA = 34°

      Сумма внутренних углов треугольника 180°. Тогда:

                     ∠AED = 180 - 2·34 = 112°

3).  Так как ∠1 + ∠2 = 180°, то a || b

        ∠4 = ∠С, как вертикальные при параллельных и секущей

        ∠С + ∠3 = 180°, как внутренние односторонние.

     Тогда: ∠С = ∠3 + 70

                  2 · ∠3 = 110

                       ∠3 = 55°    =>    ∠С = ∠4 = 180 - 55 = 125°