Предмет: Алгебра, автор: Pasha831

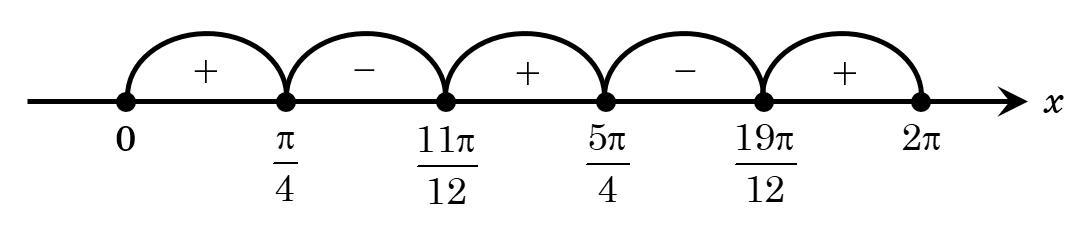
Помогите решить это неравенство. Много разных ходов перепробовал, ничего не получается...

Приложения:

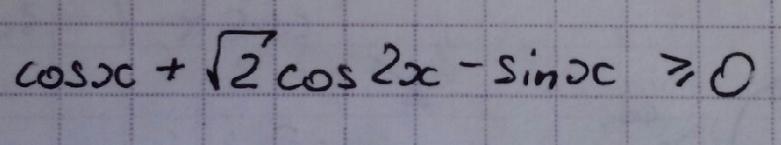
Ответы

Автор ответа: nikebod313

Решая неравенство $f(x) > 0$ (или $f(x) < 0$ , $f(x) \geq 0$ , $f (x) \leq 0$ ), где $f(x)$ — тригонометрическое выражение, которое не сводиться к простейшим тригонометрическим неравенствам, можно решить универсальным методом — методом интервалов.

Алгоритм применения метода интервалов для решения тригонометрических неравенств может быть таким:

1) представить выражение $f(x)$ в виде суммы тригонометрических функций в первой степени;

2) найти $T$ — период $f(x)$ , им будет наименьшее общее кратное периодов из слагаемых;

3) решить уравнение $f(x) = 0$ на промежутке длиной $T$ ;

4) разбить промежуток $T$ областью определения и нулями функции $f(x)$ на каждом из них;

5) в зависимости от найденных знаков с учетом периодичности $f(x)$ записать ответ.

Решим неравенство $\cos x + \sqrt{2} \cos 2x - \sin x\geq 0$ .

Наименьшим положительным периодом функции $\varphi _{1}(x) = \cos x$ является $T_{1} = 2\pi$ , функции $\varphi _{2}(x) = \cos 2x$ является $T_{2} =\dfrac{2\pi}{2} = \pi$ , а функции $\varphi _{3}(x) = \sin x$ является $T_{3} = 2\pi$ . Поэтому наименьшим положительным периодом функции $f(x) = \cos x + \sqrt{2} \cos 2x - \sin x$ будет $2\pi$ . Рассмотрим это неравенство на промежутке длиной

$\cos x + \sqrt{2}(\cos^{2}x - \sin ^{2}x) - \sin x \geq 0$

Распишем выражение $\cos^{2} x - \sin^{2}x$ как разность квадратов двух выражений по формуле: $a^{2} - b^{2} = (a - b)(a+ b)$

Имеем:

$(\cos x - \sin x)+\sqrt{2}(\cos x - \sin x)(\cos x + \sin x) \geq 0$

Вынесем общий множитель $\cos x - \sin x$ . Имеем:

$(\cos x - \sin x)(1 + \sqrt{2}(\cos x + \sin x )) \geq 0$

Упросим максимально возможно это неравенство:

$\sqrt{2}\left(\dfrac{\sqrt{2}}{2}\cos x - \dfrac{\sqrt{2}}{2}\sin x \right)\left(1 + 2 \left( \dfrac{\sqrt{2}}{2} \cos x + \dfrac{\sqrt{2}}{2}\sin x \right) \right) \geq 0$

$\left(\sin \dfrac{\pi}{4} \cos x -\cos \dfrac{\pi}{4}\sin x \right)\left(1 + 2 \left( \sin \dfrac{\pi}{4} \cos x + \cos \dfrac{\pi}{4}\sin x \right) \right) \geq 0$

$\sin \left(\dfrac{\pi}{4} - x \right) \left(1 + 2 \sin \left(\dfrac{\pi}{4}+ x \right) \right) \geq 0$

Решим уравнение $\sin \left(\dfrac{\pi}{4} - x \right) \left(1 + 2 \sin \left(\dfrac{\pi}{4}+ x \right) \right) = 0$

Полученное уравнение равносильно совокупности уравнений:

$\left[\begin{array}{ccc}\sin \left(\dfrac{\pi}{4} - x \right) = 0, \ \ \\\sin \left(\dfrac{\pi}{4} + x \right) = -\dfrac{1}{2} \\\end{array}\right$ откуда $\left[\begin{array}{ccc}x = \dfrac{\pi}{4} - \pi n, \ n \in Z \ \ \ \ \\ x = \dfrac{11\pi}{12} + 2\pi k, \ k \in Z \\x = \dfrac{19\pi}{12} + 2\pi l, \ l \in Z \ \end{array}\right$

Итак, имеем множество нулей функции $f(x)$

Рассмотрим промежуток $[0 ; \ 2\pi]$ длиной $2\pi$ . Ему принадлежат 4 нуля функции: $x_{1} = \dfrac{\pi}{4}$ , $x_{2} = \dfrac{11\pi}{12}$ , $x_{3} = \dfrac{5\pi}{4}$ , $x_{4} = \dfrac{19\pi}{12}$ . Обозначим их на числовой оси. Определим знак функции на каждом из полученных промежутков, подставляя в $f(x)$ по одному значению $x$ из каждого промежутка (см. вложение).

Дополняя к полученным промежуткам период $2 \pi$ , будем иметь множество решений неравенства:

$x \in \left[2\pi n; \dfrac{\pi}{4} + 2\pi n \right] \cup \left[\dfrac{11\pi}{12} + 2\pi n; \dfrac{5\pi}{4} + 2\pi n \right] \cup \left[\dfrac{19\pi}{12} + 2\pi n; 2\pi + 2\pi n \right], \ n \in Z$

Ответ: $x \in \left[2\pi n; \dfrac{\pi}{4} + 2\pi n \right] \cup \left[\dfrac{11\pi}{12} + 2\pi n; \dfrac{5\pi}{4} + 2\pi n \right] \cup \left[\dfrac{19\pi}{12} + 2\pi n; 2\pi + 2\pi n \right], \ n \in Z$

Приложения: