Предмет: Алгебра, автор: satanakorovka

Логарифмы~~~~

Поможете? Хоть намекнуть что-нибудь))

Приложения:

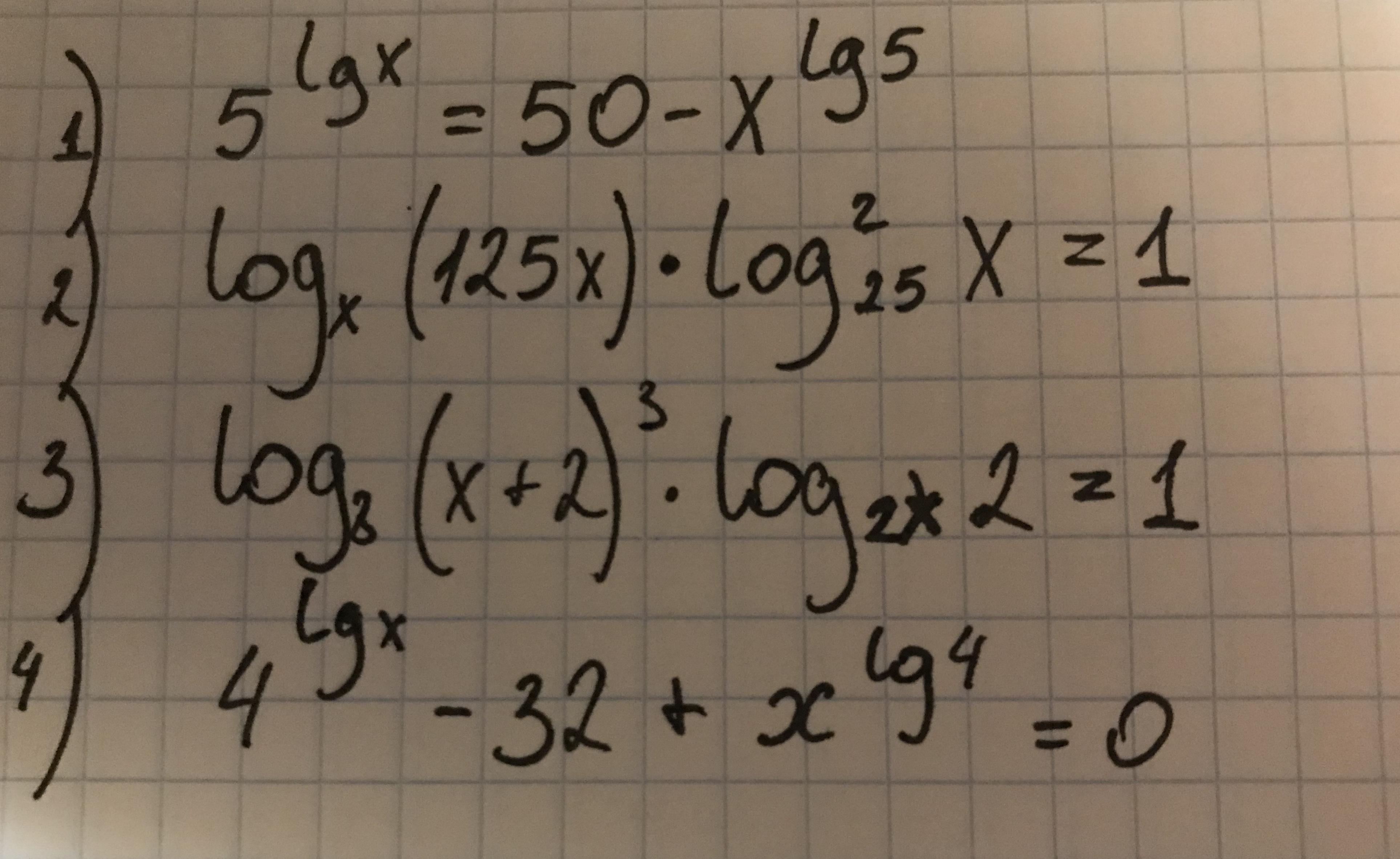
Ответы

Автор ответа: Medved23
2

1) Воспользуемся свойством a^{\log_bc}=c^{log_ba}

5^{\lg x}=50-x^{\lg5}; OD3: x>0, x\neq 1.\\\\5^{\lg x}=50-5^{\lg x},\\\\2\cdot5^{\lg x}=50,\\5^{\lg x}=25;\\\\5^{\lg x}=5^2\Rightarrow \lg x =2\Rightarrow x =10^2, x=100.

2) ОДЗ: \left \{ {{x>0} \atop {x\neq 1}} \right.

Распишем первый множитель как логарифм произведения: \log_x(125x)=\log_x125+\log_xx=1+3\log_x5=1+\frac{3}{\log_5x}

Распишем второй множитель:

\log_{25}^2x=(\log_{5^2}x)^2=(\frac{1}{2}\log_5x)^2=\frac{1}{4}\log_5^2x

Сделаем замену: \log_5x=t

Имеем уравнение

(1+\frac{3}{t})\frac{1}{4}t^2=1 \\\\\frac{1}{4}t^2+\frac{3t^2}{4t}-1=0;\\\\\frac{1}{4}t^2+\frac{3}{4}t -1=0|\cdot4,\\\\t^2+3t-4=0 \Rightarrow t_1=-4, t_2=1.\\\left \ [ {{\log_5x=-4} \atop {\log_5x=1}} \right. \Rightarrow x_1=\frac{1}{625}, x_2=5.

3) \log_8(x+2)^3\cdot\log_{2x}2=1;\\OD3:\left \{ {{x>0} \atop {x\neq 0,5}} \right.\\\\\frac{3}{3}\log_2(x+2)\cdot\frac{1}{\log_2(2x)}=1;\\\frac{\log_2(x+2)}{\log_22+\log_2x}=1,\\\\ \log_2(x+2)-1=\log_2x;\\\log_2(\frac{x+2}{2})=\log_2x\\\frac{x+2}{2}=x,\\\\2x=x+2\Rightarrow x=2.

4) OD3: \left \{ {{x>0} \atop {x\neq 1}} \right. \\\\4^{\lg x}+4^{\lg x}=32,\\\\2\cdot4^{\lg x}=32,\\\\4^{\lg x}=16,\\\\4^{\lg x}=4^2\Rightarrow \lg x =2\Rightarrow x = 10^2, x= 100.

Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Русский язык, автор: Рина82
проверочные слова к словам несется, парусах. перед проверяемым словом записать проверочное: краснота, весело, смельчак, тенистый, цветет.
2 года назад
Предмет: Українська мова, автор: DinaNatali

Добрать до поданих слів споріднені так щоб у корені звук (о) змінився на (і)

(Школа, робота, ходити, гора, нора, зоря) 
2 года назад
Предмет: Русский язык, автор: Аноним

ПОМОГИТЕ ПОЖАЛУЙСТА!!!!!                                                                     Составте шесть предоложений (среди них должны быть и простые с однородными членами,и сложными с союзами И, А, НО и  с прямой речью) К каждому виду по два предложения надо.                       ЗАРАНЕЕЕ СПАСИБО!
2 года назад
Предмет: Физика, автор: Вввввввв12345
В сосуде, из которого быстро откачивают воздух, находится 100 г воды при температуре 0°C. В результате интенсивного испарения происходит замораживание воды. В лёд обращается ...
9 лет назад
Предмет: Математика, автор: джеффиубийца
помогите со всем плизззззззззззззззз
9 лет назад