Предмет: Геометрия,
автор: vanya437
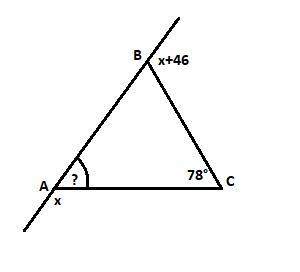
В треугольнике ABC внешний угол при вершине B на 46∘ больше внешнего угла при вершине A. Найдите угол A треугольника ABC, если угол C равен 78∘.
Ответы
Автор ответа:
6
Ответ:
∠А = 74°.
Объяснение:
Внешние углы треугольника являются смежными с внутренним при той же вершине. Смежные углы в сумме равны 180°.
Пусть внешний угол при вершине А равен х°.
Тогда внешний угол при вершине В равен (х+46)°
1. ∠А = 180°-х°, ∠В = 180° -(х+46)° =134°-х°.
Сумма внутренних углов треугольника равна 180°, значит
(180°-х) + (134°-х) + 78° = 180°. =>
х = 106° => ∠А = 180°-х = 74°.
Или так:
Сумма внешних углов треугольника равна 360°.
Тогда х + х + 46° + (180 -78)° = 360°
2х = 212°
х = 106°. =>
∠А = 180°-х = 74°.
Приложения:
Интересные вопросы
Предмет: Английский язык,
автор: vladisla1989
Предмет: Русский язык,
автор: nokoniki
Предмет: Русский язык,
автор: niki100676
Предмет: Биология,
автор: Аноним
Предмет: География,
автор: лолкеказаза1