Предмет: Алгебра, автор: DarkBrownie1

Помогите пожалуйста в решением алгебры :3

Приложения:

Ответы

Автор ответа: Medved23

0

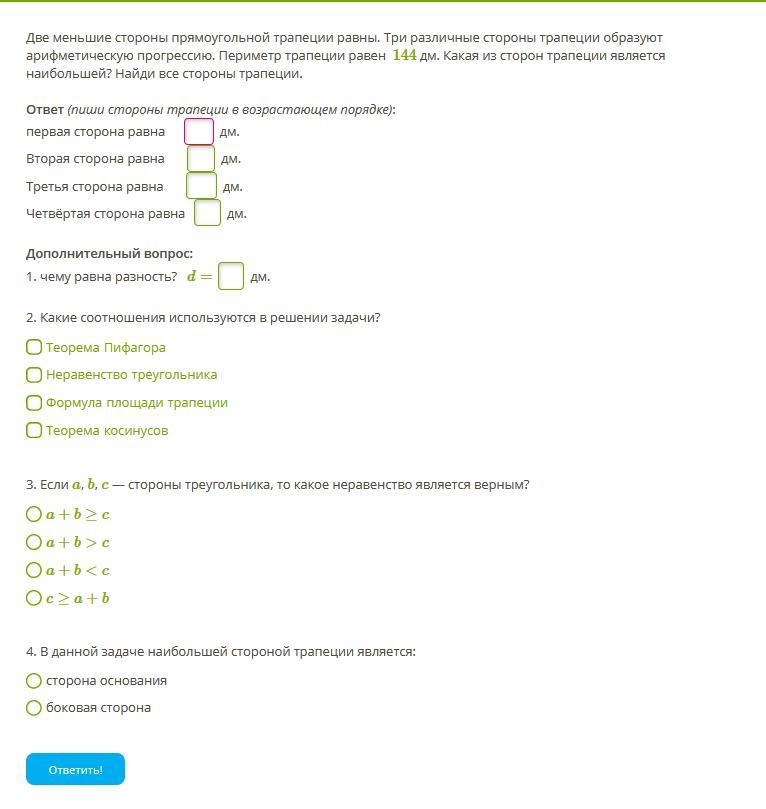
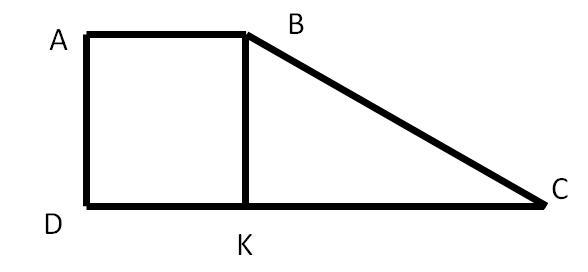
Пусть АВСD - данная трапеция, AB || CD; AB = AD; $(x_n)$ - арифметическая прогрессия.

Пусть $d$ - разность прогрессии, AB = $x_1$ По формуле $n-$ ого члена имеем: BC = $x_2=x_1+d,$ CD = $x_3=x_1+2d$

Периметр трапеции равен: $P = AB + BC + CD + AD = x_1+x_1+d+x_1+2d+x_1=4x_1+3d$ , т.е.

$4x_1+3d=144$ .

Опустим высоту BK = AD = $x_1$ ⇒ ABKD - квадрат ⇒ KD = $x_1$ ⇒ CK = CD - KD = $x_1+2d-x_1$ = $2d$ .

В ΔВКС (∠К = 90°) по теореме Пифагора: ВС² = ВК² + СК² = $x_1^2+(2d)^2=x_1^2+4d^2$ ⇒ $(x_1+d)^2=x_1^2+4d^2\Rightarrow 2x_1d=3d^2.$

Имеем систему:

$\left \{ {{4x_1+3d=144} \atop {2x_1d=3d^2}} \right.$ $\left \{ {{4x_1+3d=144} \atop {2x_1=3d}} \right. \left \{ {{6d+3d=144} \atop {x_1=\frac{3}{2}d }} \right. \left \{ {{9d=144} \atop {x_1=\frac{3}{2}d}} \right. \Rightarrow \left \{ {{d=16} \atop {x_1=24}} \right.$

Тогда AD = AB = 24 дм, BC = 24 + 16 = 40 дм, CD = 24 + 2 · 16 = 56 дм.

ОТВЕТ: 24 дм; 24 дм; 40 дм; 56 дм.

Доп. вопросы:

1. d = 16

2. Теорема Пифагора

3. Неравенство треугольника: $a + b \geq c$

4. Сторона основания (CD).

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Українська мова, автор: den417

Переказ тексту "Привиди кататроф"

2 года назад

Предмет: Другие предметы, автор: tatka123

помогите написать по музыке ::::напишите примеры самых известных апперет и расскажите кратко об одной из них!!дам много пкт!!!!

2 года назад

Предмет: Английский язык, автор: Ivan997

Ответье на вопросы.

1.Which media is the most popular in your family?

2.Have you got a radio?

3.Have you got a television?

4.Is it colour or black and white television?

5.Who in your family watches television more than others?

6.How many tv channels do you have in your area?

7.Which tv broadcasting company is your favourite ?

8.What programmes does your local tv station broadcast ?

9.Have you got satellite tv in you area ?

10.Can you watch any American or British programmes in your area?

11.Do you video some Tv programmes and watch them later?

2 года назад

Предмет: Химия, автор: rusbagrov01

Запишите формулу вещества, состоящего из:
-двух атомов цезия, одного атома кислорода
- двух атомов брома
- одного атома рубидия, одного атома кислорода

9 лет назад

Предмет: Алгебра, автор: YanaMeow1

ПОМОГИТЕ ПЛЕЕЕС. ОЧЕНЬ НУЖНО. С полными ответами.

9 лет назад