Предмет: Алгебра, автор: djalilovann19

Решите уравнение пожалуйста)

Приложения:

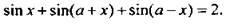
Ответы

Автор ответа: nikebod313

$\sin x + \sin(a + x) + \sin (a - x) = 2$

$\sin x + 2\sin\dfrac{a + x + a - x}{2} \cos \dfrac{a + x - a + x}{2} = 2$

$\sin x + 2\sin a \cos x = 2$

Воспользуемся универсальной тригонометрической подстановкой (при этом $2\sin a$ — число):

$\sin \alpha = \dfrac{2\text{tg}\dfrac{\alpha }{2} }{1 + \text{tg}^{2}\dfrac{\alpha }{2} }$

$\cos \alpha = \dfrac{1 - \text{tg}^{2}\dfrac{\alpha }{2} }{1 + \text{tg}^{2}\dfrac{\alpha }{2} }$

Имеем:

$\dfrac{2\text{tg}\dfrac{x}{2} }{1 + \text{tg}^{2}\dfrac{x}{2} } + 2\sin a \cdot \dfrac{1 - \text{tg}^{2}\dfrac{x}{2} }{1 + \text{tg}^{2}\dfrac{x}{2} } = 2$

Сделаем соответствующую замену: $\text{tg} \dfrac{x}{2} = t, \ x \neq \pi + 2\pi n, \ n \in Z$

Имеем:

$\dfrac{2t }{1 + t^{2} } + 2\sin a \cdot \dfrac{1 - t^{2} }{1 + t^{2}} = 2$

Решим полученное уравнение в зависимости от значений параметра $a$

$\dfrac{2t}{1 + t^{2}} + \dfrac{2\sin a (1 - t^{2})}{1 + t^{2}} - 2 = 0$

$\dfrac{2t + 2\sin a - 2t^{2}\sin a - 2 - 2t^{2}}{1 + t^{2}} = 0$

$\dfrac{-2t^{2}(1 + \sin a) + 2t + 2\sin a - 2}{1 + t^{2}} = 0$

$-2t^{2}(1 + \sin a) + 2t + 2\sin a - 2 = 0$

$2t^{2}(1 + \sin a) - 2t - 2\sin a + 2 = 0$

Если $1 + \sin a = 0$ , то есть $a = -\dfrac{\pi}{2} + 2\pi n, \ n \in Z$ , то имеем линейное уравнение:

$-2t + 2 + 2 = 0\\-2t = -4\\t = 2$

Тогда $\text{tg}\dfrac{x}{2} = 2$

$\dfrac{x}{2} = \text{arctg}2 + \pi k, \ k \in Z$

$x = 2\text{arctg}2 + 2\pi k, \ k \in Z$

Если $1 + \sin a \neq 0$ , то есть $a \neq -\dfrac{\pi}{2} + 2\pi k, \ k \in Z$ , то имеем квадратное уравнение, которое решим через дискриминант относительно $t$ .

$D = (-2)^{2} - 4 \cdot 2(1 + \sin a) \cdot (-2\sin a + 2) = -12 + 16\sin^{2}a$

Данное уравнение имеет корни, если $D \geq 0$

Определим, когда данное уравнение не будет иметь корней:

$-12 + 16\sin^{2}a < 0$

$\sin^{2}a < \dfrac{3}{4}$

$-\dfrac{\sqrt{3}}{2} < \sin a < \dfrac{\sqrt{3}}{2}$

$a \in \left(-\dfrac{\pi}{3} + \pi k; \ \dfrac{\pi}{3} + \pi k \right), \ k \in Z$

Следовательно, данное уравнение будет иметь корни, если

$\sin^{2}a \geq \dfrac{3}{4}$

$\left\{\begin{array}{ccc}\sin a \geq \dfrac{\sqrt{3}}{2}, \ \ \\\sin a \leq -\dfrac{\sqrt{3}}{2} \\\end{array}\right$

$a \in \left[-\dfrac{2\pi}{3} + \pi k; \ -\dfrac{\pi}{3} + \pi k \right]$

Тогда:

$t_{1} = \dfrac{2 + \sqrt{16\sin^{2}a - 12}}{4} = \dfrac{1}{2} + \sqrt{\sin^{2}a - \dfrac{3}{4} }$

$t_{2} = \dfrac{2 - \sqrt{16\sin^{2}a - 12}}{4} = \dfrac{1}{2} - \sqrt{\sin^{2}a - \dfrac{3}{4} }$

Сделаем обратную замену:

$\left[\begin{array}{ccc}\text{tg} \dfrac{x}{2} = \dfrac{1}{2} + \sqrt{\sin^{2}a - \dfrac{3}{4} }\\\text{tg} \dfrac{x}{2} = \dfrac{1}{2} - \sqrt{\sin^{2}a - \dfrac{3}{4} }\\\end{array}\right$

$\left[\begin{array}{ccc} \dfrac{x}{2} = \text{arctg}\left(\dfrac{1}{2} + \sqrt{\sin^{2}a - \dfrac{3}{4} }\right) + \pi l, l \in Z \ \ \ \\\dfrac{x}{2} = \text{arctg}\left(\dfrac{1}{2} - \sqrt{\sin^{2}a - \dfrac{3}{4} }\right) + \pi m, m \in Z\\\end{array}\right$

$\left[\begin{array}{ccc} x = 2\text{arctg}\left(\dfrac{1}{2} + \sqrt{\sin^{2}a - \dfrac{3}{4} }\right) + \pi l, l \in Z \ \ \ \\x = 2\text{arctg}\left(\dfrac{1}{2} - \sqrt{\sin^{2}a - \dfrac{3}{4} }\right) + \pi m, m \in Z\\\end{array}\right$

Ответ:

Если $a = -\dfrac{\pi}{2} + 2\pi n, \ n \in Z$ , то $x = 2\text{arctg}2 + 2\pi k, \ k \in Z$

Если $a \in \left[-\dfrac{2\pi}{3} + \pi k; \ -\dfrac{\pi}{3} + \pi k \right]$ , то $\left[\begin{array}{ccc} x = 2\text{arctg}\left(\dfrac{1}{2} + \sqrt{\sin^{2}a - \dfrac{3}{4} }\right) + \pi l, l \in Z \ \ \ \\x = 2\text{arctg}\left(\dfrac{1}{2} - \sqrt{\sin^{2}a - \dfrac{3}{4} }\right) + \pi m, m \in Z\\\end{array}\right$

Если $a \in \left(-\dfrac{\pi}{3} + \pi k; \ \dfrac{\pi}{3} + \pi k \right), \ k \in Z$ , то $x \in \varnothing$