Предмет: Математика, автор: 532532253

Найти интеграл рациональной функции

СРОЧНО ПОМОГИТЕ ПОЖАЛУЙСТА

Приложения:

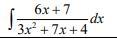
Ответы

Автор ответа: IrkaShevko
1

Ответ:

Пошаговое объяснение:

\int {\dfrac{6x+7}{(3x+4)(x+1)} } \, dx =\int {\dfrac{A}{3x+4}+\dfrac{B}{x+1} } \, dx =[A=3;B=1]=\\\\=\int {\dfrac{3}{3x+4}} \, dx +\int {\dfrac{1}{x+1}} \, dx=\int {\dfrac{1}{3x+4}} \, d(3x+4) +\int {\dfrac{1}{x+1}} \, d(x+1)=\\\\=ln|3x+4|+ln|x+1|+C

Автор ответа: Аноним
0

Решаем вторым способом, намного проще предыдущего)), просто подгоняем под знак дифференциала знаменатель.

Приложения:
IrkaShevko: не все сразу заметят ваш просто способ, мой способ универсален в данных задачах, поэтому "унижать" его глупо, не находите?
Аноним: я не унижаю ни Вас, ни Ваш способ, а подгонка под дифференциал, на мой взгляд, проще, тем более, что вряд ли человек, задавший вопрос, поймет, как найдены Ваши коэффициенты, методом неопределенных коэффициентов, или еще как.., объяснений - то по сути, нет, есть только готовые коэффициенты. Или не прав?
IrkaShevko: немного очевидно, что сумма дробей равна исходной дроби под интегралом, полагаю, что человек, изучающий высшую математику, способен приравнять две дроби и решить систему линейных уравнений с двумя неизвестными
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Русский язык, автор: rasha555

Составьте из простых предложений сложные с союзами и, а, но, запишите.

1.Небо очистилось от облаков.Луна ярко осветила лесную поляну.2.Днём пригревало солнце.Ночью морозы доходили до семи градусов.3.Ветер затих.Погода улучшилась.4.Солнце только ещё поднималось.Его лучи уже освещали верхушки деревьев.
2 года назад
Предмет: Английский язык, автор: Benetton20

Кто знает английский помогите решить!!

 раскройте скобки употребляя глаголы в present continuous или в present simple.

it usually (to take) me an hour to do my written exercises.

where boris (to be)?i (to look) for him. - he (to have) dinner.

i(to look) for a cassette recorder.you(to have) anything on sale?-take a look at this little sonic walk-man.-no,i (not to went) that kind.-well,this supersound might interest you.it (to be) a good size , it (to be) stereo and it ( to have) a radio to listen to the news.

i (not to know) about you,but i (to go) out to the cinema.
2 года назад
Предмет: Українська мова, автор: дианочичка

твир я и украинська мова пожалуста мне нужно до 15;00
2 года назад
Предмет: Биология, автор: ДашуняКизилова
Почему при динамической работе утомление наступает позже.
9 лет назад
Предмет: Химия, автор: katebantos06122002
Расположите тхимические элементы в порядки возврастания:немаллические Na, Li, K
Металл; Si, Cl, S
9 лет назад