Предмет: Алгебра,
автор: shils
решите пожалуйста вот эти примеры
Приложения:
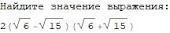
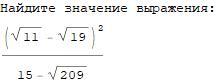

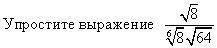
Ответы
Автор ответа:
2
Найти значение выражения:
Найти значение выражения:
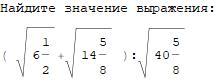
Найти значение выражения:
Найти значение выражения:
Упростить выражение:
Интересные вопросы
Предмет: Другие предметы,
автор: УмИк
Предмет: Русский язык,
автор: rigik76
Предмет: Русский язык,
автор: Даша999
Предмет: Алгебра,
автор: kalaychev66
Предмет: Алгебра,
автор: balerinaarina