Предмет: Геометрия, автор: BILFIGOR

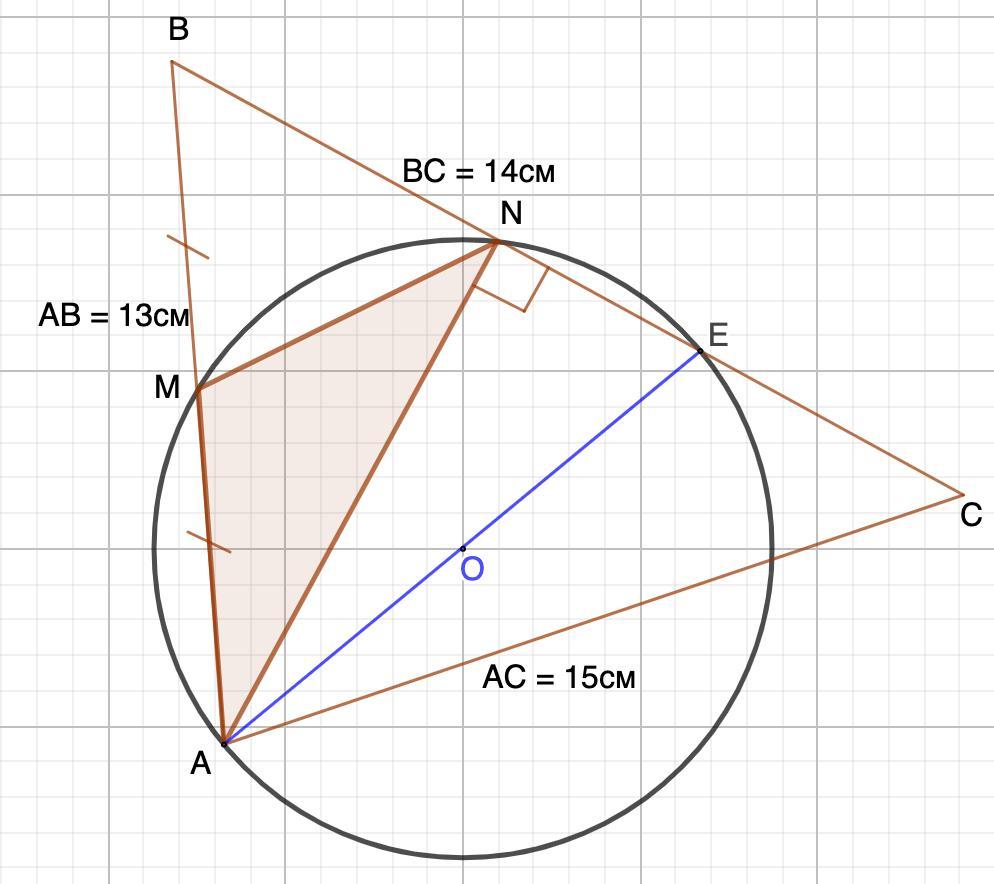
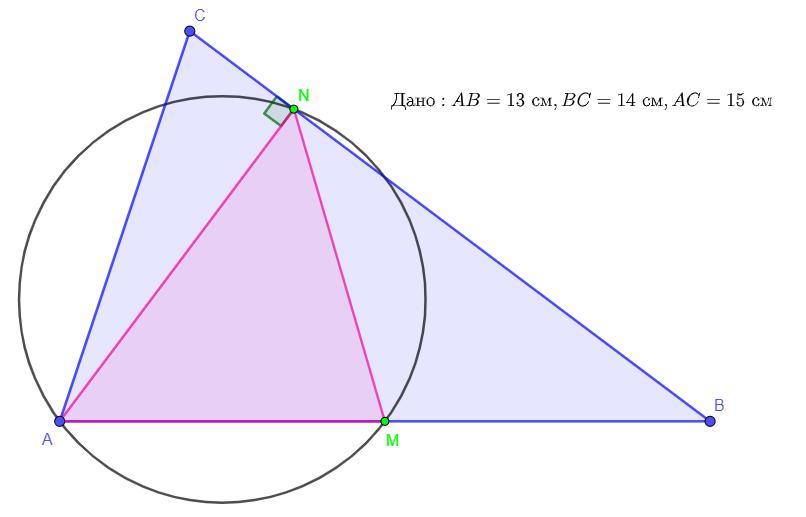
В Треугольнике ABC AB=13 см, BC=14см, AC=15 см, AN- высота, M- середина стороны AB. Найдите радиус окружности, описанной около треугольника AMN.

Ответы

Автор ответа: mathkot

Ответ:

R = 8,45 см

Объяснение:

Дано: AB = 13 см, BC = 14см, AC = 15 см, AN - высота, AM = MB

Найти: R - ?

Решение:

Пусть p - полупериметр треугольника ΔABC, тогда по определению полупериметра: $p = \dfrac{AB + BC + AC}{2} = \dfrac{13 + 14 + 15}{2} = \dfrac{42}{2} = 21$ см.

По формуле площади Герона для треугольника ΔABC:

$S_{зABC} = \sqrt{p(p - AB)(p - BC)(p - AC)} = \sqrt{21(21 - 13)(21 - 14)(21 - 15)}=$

$= \sqrt{21 \cdot 8 \cdot 7 \cdot 6} = \sqrt{7056} = 84$ см².

По формуле площади треугольника (ΔABC):

$S_{зABC} = \dfrac{AN \cdot CB}{2} \Longrightarrow AN = \dfrac{2S_{зABC} }{CB} = \dfrac{2 \cdot 84}{14} = \dfrac{84}{7} = 12$ см.

Так как по условию AM = MB и по основному свойству отрезка

AB = AM + MB, то AM = MB = AB : 2 = 13 : 2 = 6,5 см.

Так как AN - высота по условию, то треугольник ΔANB - прямоугольный и так как AM = MB по условию, то по определению отрезок NM - медиана треугольника ΔANB, тогда по теореме медиана прямоугольного треугольника проведенная к гипотенузе равна половине гипотенузы, тогда NM = AM = MB = 6,5 см.

Пусть s - полупериметр треугольника ΔAMN, тогда по определению полупериметра: $s = \dfrac{AM+ NM + AN}{2} = \dfrac{6,5 + 6,5 + 12}{2} = \dfrac{25}{2} = 12,5$ см.

По формуле площади Герона для треугольника ΔAMN:

$S_{зAMN} = \sqrt{s(s - AM)(s - NM)(s - AN)} = \sqrt{12,5(12,5 - 6,5)(12,5 - 6,5)(12,5 - 12)}=$

$= \sqrt{12,5 \cdot 6 \cdot 6 \cdot 0,5} = \sqrt{225} = 15$ см².

По формуле площади треугольника (ΔAMN):

$S_{зAMN} = \dfrac{AM \cdot MN \cdot AN}{4R} \Longrightarrow R = \dfrac{AM \cdot MN \cdot AN}{4S_{зAMN}} = \dfrac{6,5 \cdot 6,5 \cdot 12}{4 \cdot 15} =$

$= \dfrac{6,5 \cdot 6,5 \cdot 12}{4 \cdot 3 \cdot 5} = \dfrac{42,25 \cdot 12}{5 \cdot 12} = \dfrac{42,25 }{5} = 8,45$ см.

Приложения:

Автор ответа: natalyabryukhova

Ответ:

Радиус окружности, описанной около треугольника AMN, равен 8,45 см.

Объяснение:

Требуется найти радиус окружности, описанной около треугольника AMN.

Дано: ΔАВС.

AB=13 см, BC=14см, AC=15 см;

AN- высота;

АМ = МВ;

Окр.О, ОА.

Найти: ОА.

Решение:

1. Найдем BN и AN.

Рассмотрим ΔАВN - прямоугольный.

По теореме Пифагора:

AN² = AB² - BN² (1)

Рассмотрим ΔАNC - прямоугольный.

По теореме Пифагора:

AN² = AC² - CN² (2)

Пусть BN = x см, тогда CN=(14 - х) см.

Приравняем (1) и (2)

AB² - BN² = AC² - CN²

или

169 - х² = 225 - (14 - х)²

169 - х² = 225 - 196 + 28х - х²

28х = 140

х = 5

⇒ BN = 5 см.

AN² = 169 - 25 = 144

AN = 12 см.

2. Найдем NE.

Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть.

⇒ BA · BM = BE · BN

13 · 6,5 = BE · 5

BE = 13 · 1,3 = 16,9 (см)

⇒ NE = BE - BN = 16,9 - 5 = 11,9 (см)

3. Рассмотрим ΔАNE - прямоугольный.

Вписанный прямой угoл опирается на диаметр.

⇒ АЕ - диаметр.

По теореме Пифагора:

АЕ² = AN² + NE²

AE² = 144 + 141,61 = 285,61

AE = 16,9 (см)

Радиус равен половине диаметра.

ОА = 16,9 : 2 = 8,45 (см)

Радиус окружности, описанной около треугольника AMN, равен 8,45 см.

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: Хорошая1

Какой глагол относится не к тому виду, что остальные? ) вскричать б) встречать в)встрять г) воскликнуть д) все эти глаголы относятся к одному виду? Ответьте пожалуйста, спасите меня.

2 года назад

Предмет: Русский язык, автор: Демонатор

Помогите написать не большое сочинение на тему Мой любимый вид спорта борьба. Пожалуйста.