Очень туго с алгеброй вдобавок я болел знаю что надо построить график и решать но даже график построить не могу помогите с 6 и 7

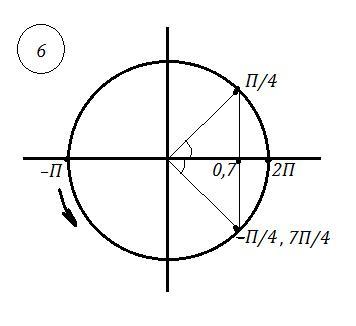
6. Найти все корни уравнения  cosx =√2 /2 , на  [ -π ; 2π] .

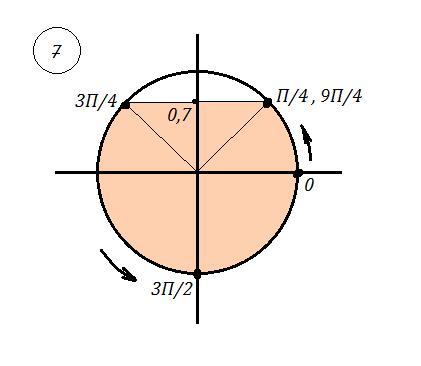
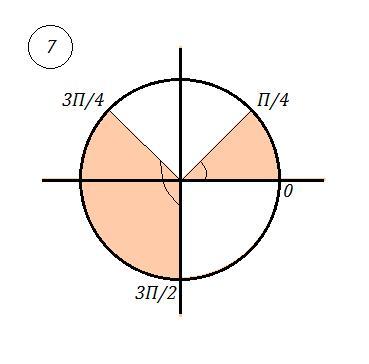
7. Найти все решения неравенства  sinx < √2 /2 ,  на  [ 0 ; 3π/2 ] .

Ответ:  6. { -π/4 ; π/4;  7π/4} .  7. x ∈  [ 0 ; π/4)  ∪  ( 3π/4 ;  3π/2] .

Объяснение:

6.  cosx =√2 /2  ,        x ∈ [ -π ; 2π] .

x = ± π/4 +2πn , n ∈ ℤ .  Из них нужно выделить  все x ∈ [ -π ; 2π]

Удобно (здесь) применить метод полного перебора.

x = { -π/4 ; π/4;  7π/4}.     * * *  при n=0 , 1   * * *

→ ---------------------------------------------------  

* * *    x₁ = -π/4 +2πn ;  x₂ = π/4 +2πn ,  n ∈ ℤ .     x₁ , x₂ ∈ [ -π ; 2π]

-π ≤-π/4 +2πn ≤ 2π ⇔ - π +π/4 ≤ 2πn ≤ 2π+π/4 ⇔ -3π/4≤2πn ≤9π/4 ⇔

-3/8≤n ≤9/8   ⇒   n = 0 ; 1   и   x₁= { -π/4; 7π/4 } .

---  аналогично  и для x₂ = π/4 +2πn  n ∈ ℤ .  x₂ ∈ [ -π ; 2π] ---

-π ≤π/4 +2πn ≤ 2π ⇔ - π -π/4 ≤ 2πn ≤ 2π - π/4 ⇔ -5π/4≤2πn ≤7π/4 ⇔

-5/8≤ n ≤7π/8  ⇒   n = 0   и   x₂= π/4 .       * * *

--------------------------------------------------  ←  

7. sinx < √2 /2                                                , x ∈ [ 0 ; 3π/2 ]

Можно  с  помощью графика  функции  y =sinx .

Учитывая  условие   x ∈ [ 0 ; 3π/2 ]  , получаем

ответ: x ∈  [ 0 ; π/4)  ∪  ( 3π/4 ;  3π/2 ] .

→ ---------------------------------------------------  

Объединение интервалов: ( -π - arcsin(√2 /2)  +2πn  ; arcsin(√2 /2) +2πn )

для всех   n ∈ ℤ .

⇔( -π - π4+2πn  ; π/4 +2πn ) ⇔ ( -5π/4 +2πn ;  π/4 +2πn )    || n=0 и n=1 ||

( -5π/4  ;  π/4 ) ∪ (3π/4 ; 9π/4)  но т.к.  x ∈ [ 0 ; 3π/2 ]  , получится  :

x ∈  [ 0 ; π/4)  ∪  ( 3π/4 ;  3π/2 ]

--------------------------------------------------  ←