Предмет: Геометрия,
автор: seowald
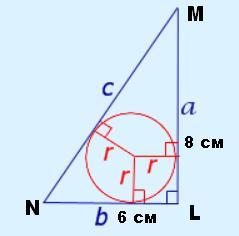
треугольник LMN, уголL=90°,NL=6, LM=8. Найдите радиус вписанной окружности.
Срочно нужно!! Заранее спасибо!
NL=6, исправил
LM=8
извиняюсь (
Так, давай ещё раз.
L=90°, NL=6, LM=8. Есть ещё известные углы?
И если есть рисунок, какая из сторон короткая, какая длинная?
L=90°, NL=6, LM=8. Есть ещё известные углы?
И если есть рисунок, какая из сторон короткая, какая длинная?
нету, как и самого рисунка.
ОК, тут просто. щас напишу
Ответы
Автор ответа:
201
Ответ:
r = (LN + LM - NM) / 2 = (6 + 8 - 10) / 2 = 4/2 = 2 см
Объяснение:
Угол L = 90°, значит треугольник прямоугольный.
Нам также известны две стороны (два катета)
LN=6 см, LM=8 см
1) Поскольку треугольник прямоугольный, то гипотенузу мы можем найти по теореме Пифагора "Квадрат гипотенузы равен сумме квадратов катетов": с² = a² + b²
В нашем треугольнике это
NM² = LN² + LM²
NM² = 6² + 8² = 36 + 64 = 100 см²
NM = √100 = 10 см
2) Далее радиус окружности находим по формуле "радиуса окружности, вписанной в прямоугольный треугольник": r = (a + b - с) / 2
r = (LN + LM - NM) / 2 = (6 + 8 - 10) / 2 = 4/2 = 2 см
Приложения:
Интересные вопросы
Предмет: Русский язык,
автор: TurqanNariman
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: назарі
Предмет: Алгебра,
автор: saeroner23
Предмет: Математика,
автор: никита2722
Что из них угол, что сторона?