Предмет: Математика, автор: panheadraven

Нужна помощь в определении сходимости интеграла​

Приложения:
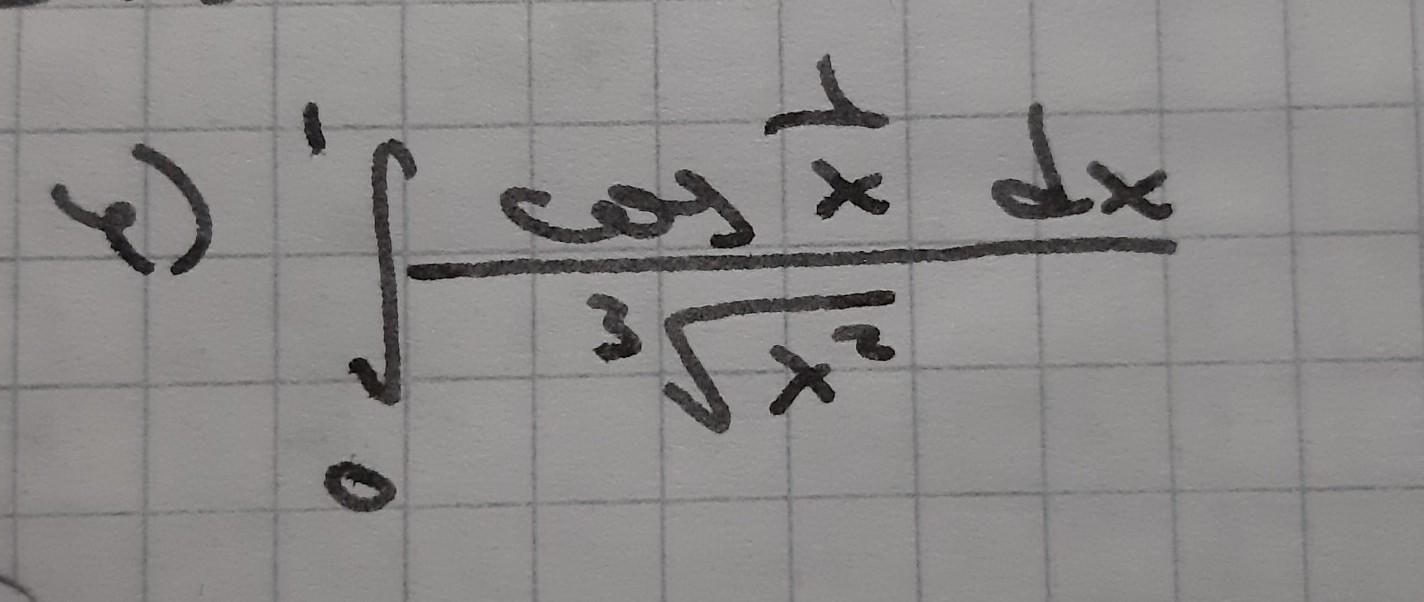
Аноним: какой аргумент у косинуса?
panheadraven: я так понимаю, что (1/x)
panheadraven: задача мне была дана именно в таком виде, так что более точно ответить не смогу

Ответы

Автор ответа: Аноним
1

Ответ:

интеграл сходится

Пошаговое объяснение:

Воспользуемся теоремой сравнения:

Сравним данный интеграл с

\int\limits^1_0 {\frac{1}{\sqrt[3]{x^2} } } \, dx=\int\limits^1_0 {x^{-\frac{2}{3 } }} \, dx= \lim\limits_{a \to 0} 3x^\frac{1}{3} \ |^1_a =\lim\limits_{a \to 0} (3-3a^\frac{1}{3})=3-0=3

который сходится.

Так как косинус изменяется от -1 до 1, то

{\frac{cos\frac{1}{x} }{\sqrt[3]{x^2} } } \leq {\frac{1}{\sqrt[3]{x^2} } }

Значит и исходный интеграл тоже сходится

panheadraven: Спасибо вам большое!
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Українська мова, автор: 380673381262
написати план до казки сомяний бичок
2 года назад
Предмет: Русский язык, автор: z5z

морфологический разбор на сосне
2 года назад
Предмет: Английский язык, автор: jul1

помогите ответить на бональные вопросы по англ)) 1..what do you spend your money on? 2..what time do you have to be at home in the evening& 3..what do you do in your free time? 4.do you have to wear a uniform? 5..how much homework do you have? 6..do you enjoy school? 7..what do you like about being a teen? 8..do you feel safe in your city?
2 года назад
Предмет: Математика, автор: yanafilonenko2
в столовой Гриша купил 2 пирожков и 3 конфеты и заплатил 41 рубль . Женя купил 5 пирожков и 6 конфет и заплатил 92 рубля . сколько рублей Коля должен вернуть жене?
9 лет назад
Предмет: Математика, автор: патимат49
16км-8км 060мпожайлуста
9 лет назад