Предмет: Математика, автор: harlan2001

Вычислить приделы с помощью правила Лопиталя

Приложения:

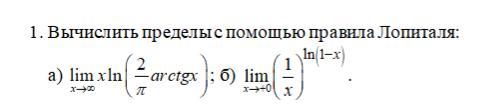
Ответы

Автор ответа: igorShap

$\lim\limits_{x\to\infty} xln(\dfrac{2}{\pi}arctgx)=\lim\limits_{x\to\infty} \dfrac{ln(\dfrac{2}{\pi}arctgx)}{\frac{1}{x}}=\lim\limits_{x\to\infty} \dfrac{\frac{1}{(\frac{2}{\pi}arctgx)}*\frac{2}{\pi}*\frac{1}{1+x^2}}{-\frac{1}{x^2}}=\\ =-\lim\limits_{x\to\infty} \frac{1}{arctgx}*\frac{x^2}{1+x^2}=-\dfrac{2}{\pi}*1=-\dfrac{2}{\pi}$

$\lim\limits_{x\to+0}x^{-ln(1-x)}=\lim\limits_{x\to+0}(e^{lnx})^{-ln(1-x)}=\lim\limits_{x\to+0}e^{-ln(1-x)lnx}=(*)\\ \lim\limits_{x\to+0}({-ln(1-x)lnx)}=\lim\limits_{x\to+0}\dfrac{-ln(1-x)}{\frac{1}{lnx}}=\lim\limits_{x\to+0}\dfrac{\frac{1}{1-x}}{-\frac{1}{xln^2x}}=\lim\limits_{x\to+0}\dfrac{ln^2x}{1-\frac{1}{x}}=\lim\limits_{x\to+0}\dfrac{\frac{2lnx}{x}}{\frac{1}{x^2}}=\lim\limits_{x\to+0}\dfrac{2lnx}{\frac{1}{x}}=2\lim\limits_{x\to+0}\dfrac{\frac{1}{x}}{-\frac{1}{x^2}}=0\\ (*)=e^0=1$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: Aleexandra

Определите тип предложения: Остаток дня тянулся для Захара нестерпимо долго,и когда, солнце зашло и серые тени стали всё гуще закрывать землю вокруг,он почувствовал облегчение.

2 года назад

Предмет: Русский язык, автор: Аноним

Зачеркните лишние слова.

Неожиданный сюрприз;

электорат избирателей;

весь цвет элиты;

саммит на высшем уровне;

свободная вакансия;

самый лучший студент;

иммунитет неприкосновенности;

главный приоритет;

полный аншлаг;

глубокий сон

2 года назад

Предмет: Русский язык, автор: nataliymay

пожалуйста помогите найти 5 названий елочных игрушек начинающих с мягкого согласного звука и 5 начинающих с твердого согласного звука

2 года назад

Предмет: Литература, автор: evabo00

Ребят, привет! Очень нужно помогите. 7-10 фразеологизмов из сказки "Конек гарбунок" ЗАРАНЕЕ СПАСИБО

9 лет назад

Предмет: Литература, автор: рахима2

что значит желтый одуванчик будет и седой

9 лет назад