Предмет: Алгебра, автор: ВладимирБ

Решить уравнение
....................................

Приложения:

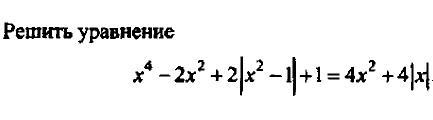
Ответы

Автор ответа: Evgenia4836

1

Решение во вложении:

Приложения:

Аноним: Слабенько

Автор ответа: Аноним

2

$x^4-2x^2+2|x^2-1|+1=4x^2+4|x|\\ \\ x^4-2x^2+1+2|x^2-1|+1=4x^2+4|x|+1\\ \\ \Big(|x^2-1|+1\Big)^2=\Big(2|x|+1\Big)^2\\ \\ \Big(|x^2-1|+1\Big)^2-\Big(2|x|+1\Big)^2=0\\ \\ \Big(|x^2-1|+1-2|x|-1\Big)\Big(|x^2-1|+1+2|x|+1\Big)=0\\ \\ \Big(|x^2-1|-2|x|\Big)\Big(|x^2-1|+2|x|+2\Big)=0$

Произведение равно нулю в том случае, когда хотя бы один из множителей равно нулю

$|x^2-1|-2|x|=0\\ \\ |x^2-1|=2|x|~~~\Rightarrow~~~ \Big(x^2-1\Big)^2=4x^2~~\Rightarrow~~ \Big(x^2-1\Big)^2-4x^2=0\\ \\ \Big(x^2-2x-1\Big)\Big(x^2+2x-1\Big)=0$ $x^2-2x-1=0\\ D=4+4=8;~~\sqrt{D}=2\sqrt{2}\\ x_{1,2}=\dfrac{2\pm2\sqrt{2}}{2}=\boxed{1\pm\sqrt{2}}$ $x^2+2x-1=0\\ D=4+4=8;~~\sqrt{D}=2\sqrt{2}\\ x_{1,2}=\dfrac{-2\pm2\sqrt{2}}{2}=\boxed{-1\pm\sqrt{2}}$

$|x^2-1|+2|x|+2=0$

Это уравнение решений не имеет, поскольку его левая часть положительная.

Ответ: $1\pm\sqrt{2};~ -1\pm\sqrt{2}$ .

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Українська мова, автор: 243225

написати 5 предложений з прислівниками.

2 года назад

Предмет: Русский язык, автор: L999

Небольшое сочинение на тему уборки школьной территории

2 года назад

Предмет: Русский язык, автор: 1000Sergey0001

Морфемный и морфологический разбор наречия (ясно).

2 года назад

Предмет: Обществознание, автор: AlaHbaBaH

Какой смысл юристы вкладывают в понятие общественные блага?
Помогите пожалуйста, очень нужно. Заранее спасибо.

9 лет назад

Предмет: Алгебра, автор: katrusia1705

игральную кость бросают дважды. Найдите вероятность того что наибольшее из двух выпавших чисел равно 5

9 лет назад