Предмет: Алгебра, автор: kpolyakova

Помогите решить пожалуйста

Приложения:

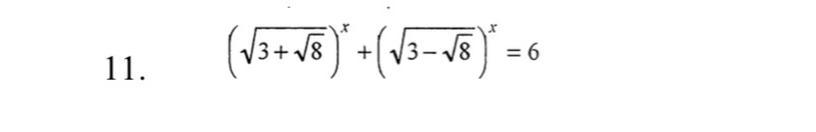
Ответы

Автор ответа: nafanya2014
0

\sqrt{3+\sqrt{8} }\cdot \sqrt{3-\sqrt{8} }=\sqrt{3^2-(\sqrt{8})^2 } =1\Rightarrow \sqrt{3+\sqrt{8} }=\frac{1}{\sqrt{3-\sqrt{8} } }

Замена переменной:

(\sqrt{3+\sqrt{8} })^{x}=t} ;\\\\(\sqrt{3-\sqrt{8} })^{x}=\frac{1}{t}

t+\frac{1}{t}=6

t^2-6t+1=0

D=36-4=32

√D=4√2

t=3-2√2=3-√8; t=3+2√2=3+√8

(\sqrt{3+\sqrt{8} })^{x}= 3-\sqrt{8} ;\\\\(\sqrt{3+\sqrt{8} })^{x}= (3+\sqrt{8})^{-1}\\\\\frac{x}{2} =-1\\\\x=-2

(\sqrt{3+\sqrt{8} })^{x}= 3+\sqrt{8} ;\\\\(\sqrt{3+\sqrt{8} })^{x}= (3+\sqrt{8})^{1}\\\\\frac{x}{2} =1\\\\x=2

О т в е т. -2; 2

kpolyakova: это неправильный ответ :(
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Русский язык, автор: svet5

 в данных предложениях опредили склонение и падеж каждого существительного.  По улице идет мальчик с портфелем в руках. В темноте не видно  что одна пуговица вырвана с мясом //  а на шарфе черное пятно , Помогите хочу себя проверить   СПАСИБО
2 года назад
Предмет: Русский язык, автор: Аноним

ПОМОГИТЕ СРОЧНО ПРОШУ !!!!!!!!!!!!

НАПИШИТЕ КРАСИВЫЕ ПРЕДЛОЖЕНИЕ С ВОДНЫМИ СЛОВАМИ 5 ПРЕДЛОЖЕНИЙ!!!!!
2 года назад
Предмет: Русский язык, автор: ALEXEY95972000

СРОЧНО ПО РУССКОМУ языку!!!!!!!!!!!11 Ландыш Чернеет лес, теплом разбуженный, Весенней сыростью объят. А уж на ниточках жемчужины От ветра каждого дрожат. Бутонов круглые бубенчики Еще закрыты и плотны, Но солнце раскрывает венчики У колокольчиков весны. Природой бережно спеленатый, Завернутый в широкий лист, Растет цветок в глуши нетронутой, Прохладен, хрупок и душист. Томится лес весною раннею, И всю счастливую тоску, И все свое благоухание Он отдал горькому цветку. Помогите ВОТ задания !!! 1) Составьте СХЕМУ П О С Л Е Д Н Е Г О предложения! 2)Выпишите все ПРИЧАСТИЯ И ПРИЛАГАТЕЛЬНЫЕ!!!!!
2 года назад
Предмет: Математика, автор: Ева12345678910111
решите срочно надо ,а то сессию не закрою,помогите!!!
9 лет назад
Предмет: Химия, автор: Riwerq
решите нужно срочно, 3,5,6,8,9,12,14
9 лет назад