Предмет: Алгебра, автор: komarik654321585

помогите пожалуйста​

Приложения:

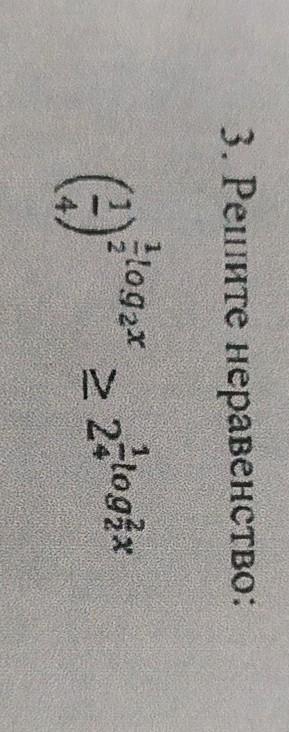
Ответы

Автор ответа: Аноним
0

Ответ:

x \in [\frac{1}{16};1]

Объяснение:

ОДЗ: x>0

Решение:

\left(\frac{1}{4} \right)^{\frac{1}{2}\log_2x} \geq 2^{\frac{1}{4}\log^2_2x} \\ \\ \left(2^{-2} \right)^{\frac{1}{2}\log_2x} \geq 2^{\frac{1}{4}\log^2_2x} \\ \\ 2^{-\log_2x} \geq 2^{\frac{1}{4}\log^2_2x} \\ \\ -\log_2x\geq \frac{1}{4}\log^2_2x \\ \\ \frac{1}{4}\log^2_2x \leq -\log_2x \ \ |*4 \\ \\ \log^2_2x \leq -4\log_2x \\ \\ \log^2_2x+4\log_2x \leq 0 \\ \\ \log_2x(\log_2x+4)\leq 0

\left[ \begin{gathered} \log_2x=0\\ \log_2x+4=0\end{gathered} \right. \Leftrightarrow \ \left[ \begin{gathered} x=2^0\\ \log_2x=-4\end{gathered} \right. \Leftrightarrow \ \left[ \begin{gathered} x=1\\ x=2^{-4}\end{gathered} \right. \Leftrightarrow \ \left[ \begin{gathered} x=1\\ x=\frac{1}{16} \end{gathered} \right.

(0)++++[\frac{1}{16}]----[1]++++>_x

x \in [\frac{1}{16};1]

Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Русский язык, автор: Анастасия2007

Написать небольшой текс-повествование"Моё утро" или "Дорога в школу. В текст нужно включить несклоняемые имена существительные кофе, пальто, шоссе, метро, такси, кафе, фтелье, пианино, фойе, согласованные с прилагательными.
2 года назад
Предмет: Русский язык, автор: SyperMena

Помогите..... Написать сочинение миниатюру "Зима" до 10 предложений с однородными членами предложения.****
2 года назад
Предмет: Русский язык, автор: leon000

Напишите по 4 сложных предложения со словами умный,глубокий.
2 года назад
Предмет: Физика, автор: pisaroglodanila
как определить погрешность измерения?
9 лет назад
Предмет: Математика, автор: Altynbekova9899
Помогите пожалуйстарешитьэто: Интеграл arccos3xdx
9 лет назад