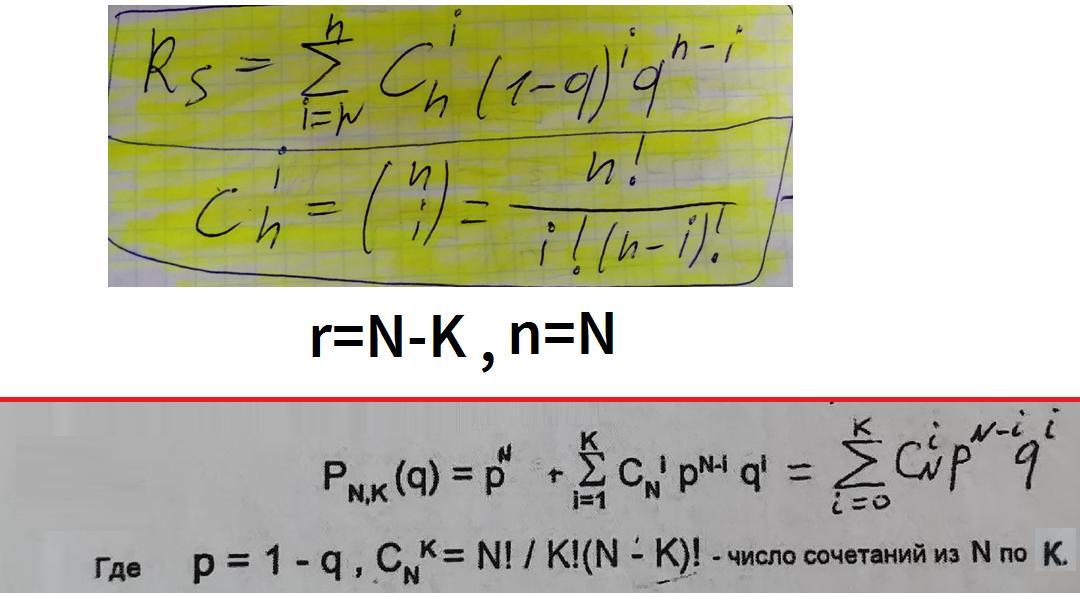
Помогите из формул сверху вывести формулу после красной черты. Это ряды и я хз как их делать.

Ответ:

Пошаговое объяснение:

Возьмём общую формулу Pk=C(n,k)*p^k*q^(n-k) и подставим в неё k=0. Так как C(n,0)=n!/[0!*(n-0)!]=n!/n!=1 и p^0=1, то P0=1*q^(n-0)=q^n. Поэтому ∑С(n,k)*p^k*q^(n-k)=q^n+∑С(n,k)*p^k*q^(n-k), где в первой сумме k изменяется от 0 до n, а в последней - от 1 до n. Поменяв теперь p и q местами, получим ∑C(n,k)*q^k*p^(n-k)=p^n+∑C(n,k)*q^k*p^(n-k). Заменив, наконец, k на i, приходим к доказываемому тождеству.