Предмет: Математика, автор: 1448smile

Элементы высшей математики. Интегралы.

Приложения:

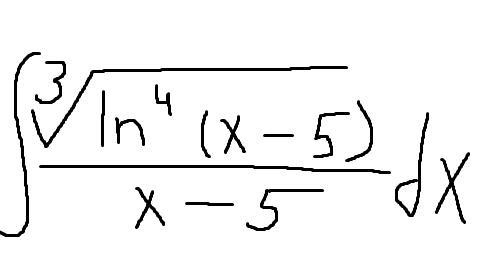
Ответы

Автор ответа: AoiK

Ответ:

$\frac{3ln^2(x-5)*\sqrt[3]{ln(x-5)} }{7}+c$

Пошаговое объяснение:

$\int\limits {\frac{\sqrt[3]{ln^4(x-5)} }{x-5} } \, dx = \int\limits {\frac{ln^{\frac{4}{3} } (x-5) }{x-5} } \, dx = \frac{3ln^2(x-5)*\sqrt[3]{ln(x-5)} }{7}+c$

Winner1919: Доброго времени суток! Вы умеете такое решать? https://znanija.com/task/37041536

Автор ответа: Alexаndr

$\displaystyle\int\frac{\sqrt[3]{ln^4(x-5)}}{x-5}dx=\int\sqrt[3]{ln^4(x-5)}d(ln(x-5))=\\=\frac{3\sqrt[3]{ln^7(x-5)}}{7}+C$

Winner1919: Доброго времени суток! Вы умеете такое решать? https://znanija.com/task/37041536

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: вааааууу

лексический разбор слова СЧАСТЬЕ в предложении "этот символ любви и счастливого конца сказки"

2 года назад

Предмет: Русский язык, автор: Аноним

Подберите к именам существительным подходящие по смыслу имена прилагательные и напишите словосочетания. Бурый медведь, ............ картина, .......... класс, .......... солнце, ......... автомобиль, ............ завтрак, .......... чувство, ............ газета, ......... молоко, ....... лестница, .......... одежда, ........... народ, ........... корзина.

2 года назад

Предмет: Английский язык, автор: Дима31

напишите сочинение на тему: Падение метеорита в челябинске 20 сентября для 6 класса можно на английском но можно и на русском

2 года назад

Предмет: Математика, автор: LeRa2004112017

У мамы 2 яблока и 3 груши.Каждый день в течении 5 дней подряд она выдаёт по одному фрукту.Сколькими способами это может быть сделано?

9 лет назад

Предмет: Физика, автор: nnknnk

Срочно

Средняя скорость движения электричек по кольцевой железной дороге протяжённостью 50 км равна 40 км/ч в обоих направлениях, причём на каждом из них интервал времени между соседними поездами составляет 5 мин. Машинист одной из электричек решил посчитать количество встреч с поездами, которые проезжают мимо него за время совершения им полного оборота. Какое число у него получилось, если последняя встреча произошла до того, как он завершил полный оборот?

9 лет назад