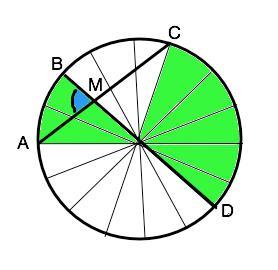
Окружность разделена точками А, В, С, и D так, что AB:BC:CD:AD = 2:3:5:6. Проведены хорды АС и BD, пересекающиеся в точке М. Определить ∠АМВ.

1)AB:BC:CD:DA=2:3:5:6, значит AB=2X,BC=3X,CD=5X,DA=6X, составим уравнение:
2X+3X+5X+6X=360
16X=360
X=22,5
AB=45°,BC=67°5`,CD=112°5`,DA=135°
2)

Ответ: 78,75°

Объяснение:   Примем коэффициент отношения дуг равным х. Тогда сумма дуг 2х+3х+5х+6х=360° ( градусной мере окружности) =>  х=360°:16=22,5°

Дуга АВ=2•22,5°=45°

Дуга СD=5•22,5°=112,5°

   Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Угол АМВ=(дуга АВ+дуга СD):2=(112,5°+45°):2=78,75°