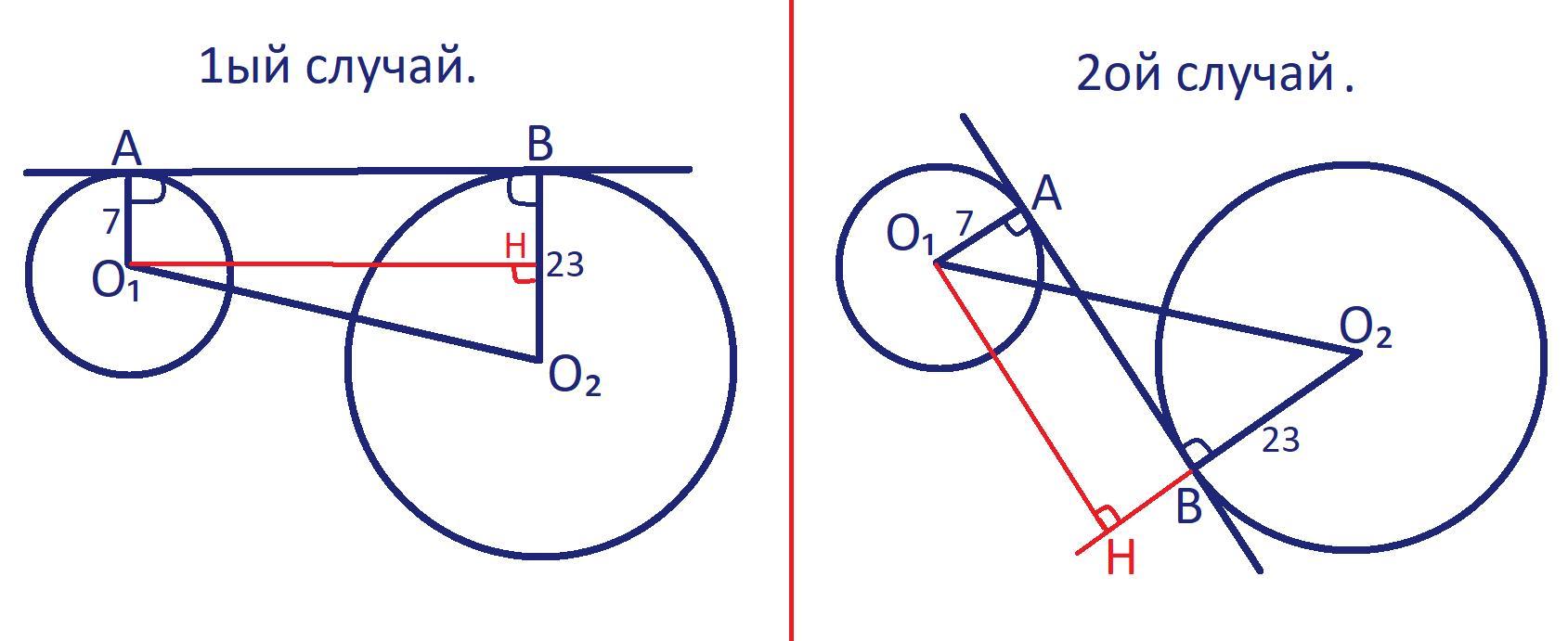
Какой может быть длина отрезка общей касательной к двум окружностям, заключенного между точками касания, если радиусы окружностей равны 23 и 7 а расстояние между центрами окружностей равно 34

Ответ: 30 или 16.

Пусть центры окружностей O₁ и O₂, а точки касания общей касательной с окружностями A и B соответственно. O₁A = 7;  O₂B = 23 - радиусы окружностей. O₁O₂ = 34 - расстояние между центрами.

• Радиус проведённый в точку касания перпендикулярен касательной.

⇒ AB⊥O₂B  и  AB⊥O₁A;

Пусть O₁H⊥O₂B  и  H∈O₂B;

AO₁O₂B - прямоугольник т.к. три прямых угла,

• Противоположные стороны прямоугольника равны между собой.

O₁A = HB = 7;

AB = O₁H  ⇒  необходимо найти O₁H.

Рассмотрим 1 случай, когда O₁, O₂ находятся в одной полуплоскости от AB.

O₂H = O₂B-HB;

O₂H = 23-7 = 16.

В прямоугольном △O₂HO₁ по теореме Пифагора:

O₁O₂² = O₁H²+O₂H²;

O₁H² = O₁O₂²-O₂H²;

O₁H² = 34²-16² = (34-16)(34+16) по формуле разности квадратов;

O₁H² = 18·50 = 2·9·2·25;

O₁H² = (2·3·5)² = 30²;

O₁H = 30.

Рассмотрим 2 случай, когда O₁, O₂ находятся в разных полуплоскостях от AB.

O₂H = O₂B+HB;

O₂H = 23+7 = 30.

В прямоугольном △O₂HO₁ по теореме Пифагора:

O₁O₂² = O₁H²+O₂H²;

O₁H² = O₁O₂²-O₂H²;

O₁H² = 34²-30² = (34-30)(34+30) по формуле разности квадратов;

O₁H² = 4·64;

O₁H² = (2·8)² = 16²;

O₁H = 16.