пожалуйста, 1 задача

Объяснение:

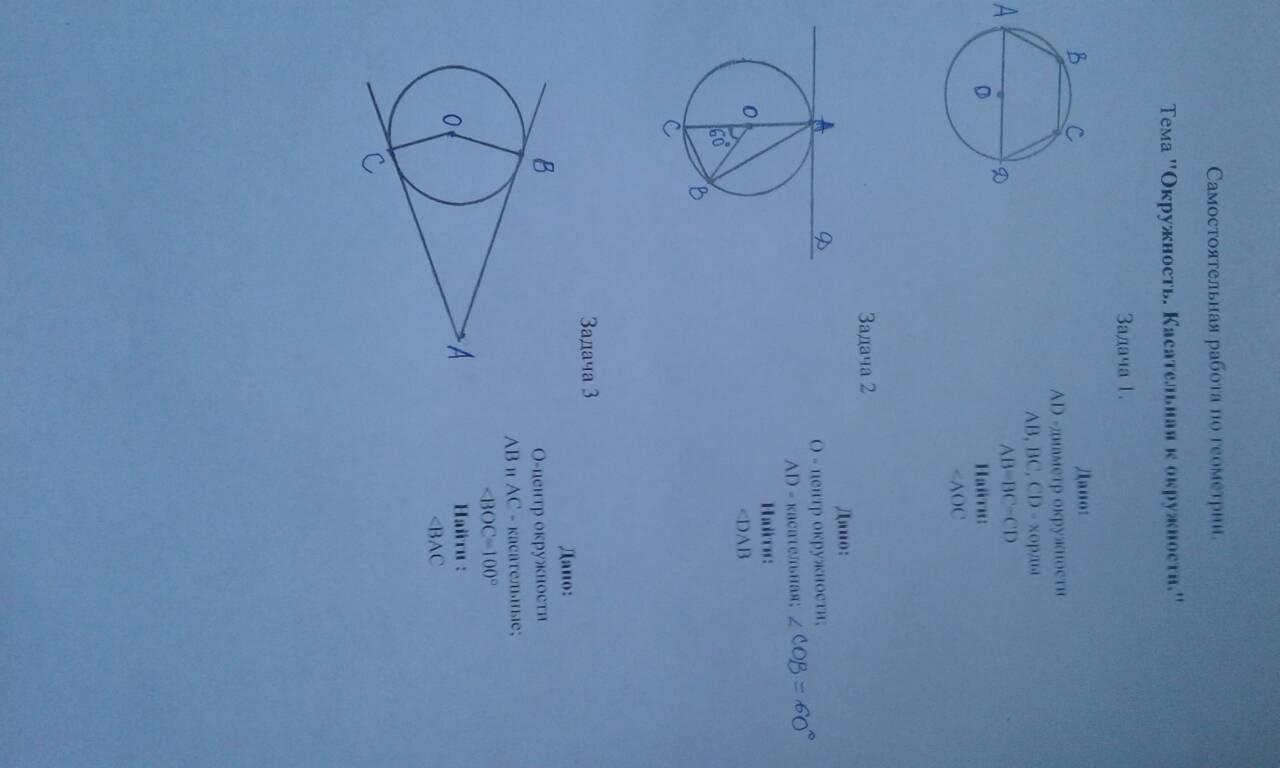
1)ΔАОВ=ΔВОС=ΔСОД по трем сторонам : АВ=ВС=СД по условию, ОА=ОВ=ОС=ОД как радиусы.

В равным треугольниках соответственные элементы равны , значит  ∠АОВ=∠ВОС=∠СОД. Обозначим равные углы  х .

∠АОВ+∠ВОС+∠СОД=180 или   3х=180, х=60

Значит ∠АОС=120°.

2)Т.к. АД-касательная , то св. касательной ОА⊥АД и ∠ДОА=90°.

Для  ΔАОВ-равнобедренного ( ОА=ОВ как радиусы),

угол   ∠СОВ-внешний. По т. о внешнем угле ∠СОВ=∠ОАВ+∠ОВА , или 60°=∠ОАВ+∠ОВА.  Но  в равнобедренном треугольнике ∠ОАВ=∠ОВА , значит ∠ОАВ=∠ОВА=30°.

∠ДАВ=∠ДОА- ∠ОАВ  или ∠ДАВ=90-30=60.

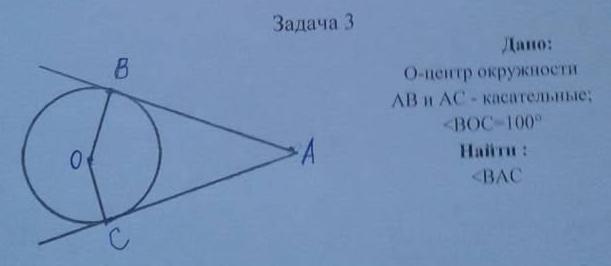
3) Т.к. АВ и АС- касательные , то св. касательной АВ⊥ОВ и  АС⊥ОС . Значит ∠АВО=90° и ∠АСО=90°  .

Сумма углов 4-х угольника равна 360°,

∠ВАС=360°-90°-90°-100°=80°