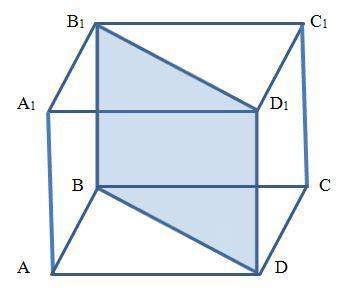
Дана правильная прямая четырехугольная призма. В основании квадрат. Площадь диагонального
сечения равна 110. Боковое ребро равно 11. Найти площадь боковой поверхности призмы.

Ответ:

80√2

Объяснение:

Sbb1d1d=110

DD1=11

так как в диагональное сечение прямоугольник, то ВD= S/DD1=110/11=10

Диагональ  квадрата  создает внутри него  равнобедренный прямоугольный треугольник  с катетами  в виде его сторон и диагональю, как  гипотенузой , из чего можно вывести следующую теорему Пифагора:

a^2+a^2=d^2

2a^2=d^2 a=√d^2/2=√10^2/2=√50 =AB=AD

Sбок= a*h+a*h+a*h+a*h=4a*h= 4*√50*10=40*√50=40*5√2=80√2