Знайдіть кути опуклого п'ятикутника, якщо вони пропорційні числам
3:5:7:9:12
Ответы
Ответ:
45°; 75°; 105°; 135°; 180°
Объяснение:
Найти углы выпуклого пятиугольника , если они пропорциональны числам 3: 5: 7: 9: 12.
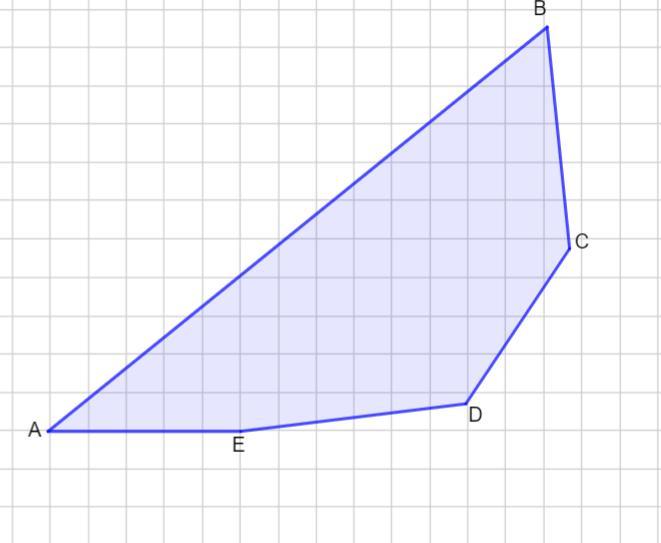
Пусть дан пятиугольник ABCDE.
Найдем сумму всех внутренних углов выпуклого пятиугольника по формуле: , где n - количество углов.
В нашей задаче n=5, так как задан пятиугольник
Тогда сумма будет равна
По условию углы пятиугольника пропорциональны числам
3: 5: 7: 9: 12, то есть
∠A : ∠B: ∠C: ∠D:∠E =3: 5: 7: 9: 12.
Тогда найдем сумму частей
3+ 5+ 7 + 9 + 12 =36 ( частей) - всего .
На эти 36 частей приходится 540°. Тогда найдем сколько градусов составляет одна часть.
540°: 36 =15° - составляет одна часть
Найдем все углы выпуклого пятиугольника
- градусная мера ∠A
- градусная мера ∠В
- градусная мера ∠С
- градусная мера ∠D
- градусная мера ∠Е
#SPJ5