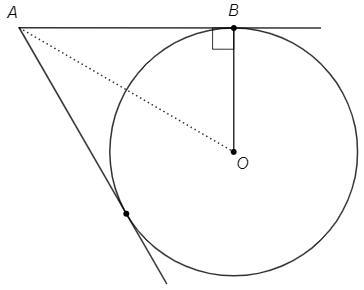
УМОЛЯЯЮ, ПОМОГИТЕ, ПОСЛЕДНЯЯ НАДЕЖДА НА ВАС, БЫЛА БЫ БЕЗУМНО БЛАГОДАРНА, ПРАВДА. С ИНЕТА НЕЛЬЗЯ, САМИ, УМОЛЯЮ. Стороны угла А касаются окружности с центром О радиуса r. Найдите: а) ОА, если r = 5 см, ∠A=60°; б) r, если ОА= 14 дм, ∠A=90°. ГЕОМЕТРИЯ, 8 КЛАСС.
Ответы
Ответ:5см
Объяснение: a) Смотри, так как угол А равен 60 градусов, а радиус равен 5 см, а угол А касается окружность, то можно мысленно представить прямой треугольник( назовем его АBO), прочертив отрезок от центра окружности О до точки касания угла к окружности. Теперь рассмотрим треугольник АBO, у которого угол А равен 60 градусов, радиус равен 5 см, а BO 90 градусов( потому что в точке пересечения отрезка к окружности получается всегда два прямых угла с разных сторон))( BO тоже является радиусом). и так, следовательно угол O равен 90-60=30 градусов, а катет лежащий против угла в 30 градусов равен половине гипотенузы), значит АО равняется 5*2=10см
a)
Окружность вписана в угол, центр лежит на биссектрисе.
BAO=A/2 =60°/2 =30°
Радиус в точку касания перпендикулярен касательной.
OBA=90°
Катет против угла 30 равен половине гипотенузы.
OA=2OB =5*2 =10 (см)
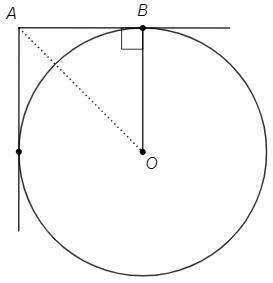
б)
BAO=A/2 =90°/2 =45°
Прямоугольный треугольник с углом 45° - равнобедренный.
△ABO - равнобедренный, AB=OB =r
Теорема Пифагора
AB^2 +OB^2 =OA^2 => 2r^2 =14^2 => r= 14√2 (дм)