Помогите сделать 3 задание

Доказательство:

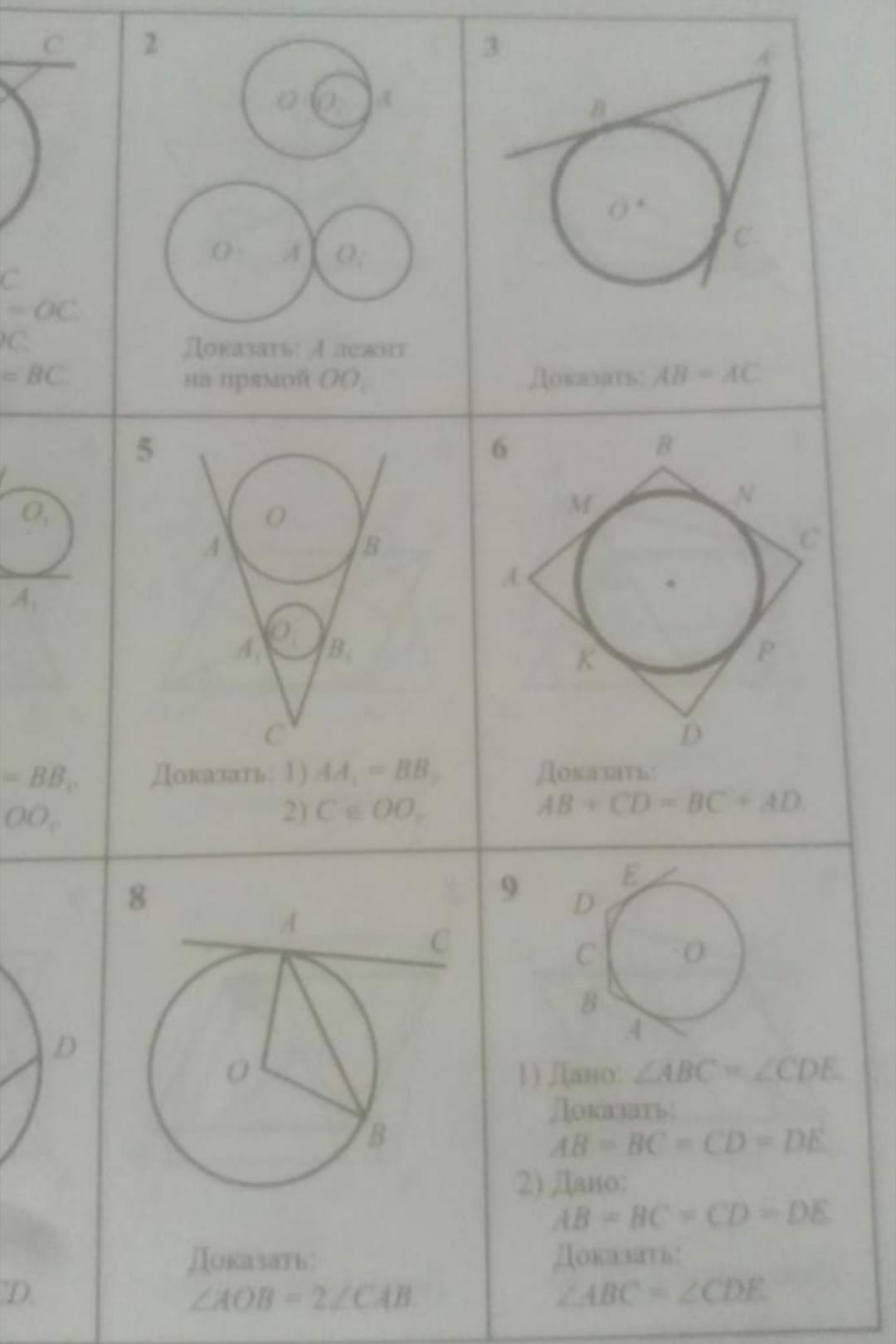
1) Треугольники AOB и AOC - прямоугольные, так как касательные к окружности перпендикулярны радиусу.

Докажем их равенство:

2.1) Проведем отрезок AO; сторона AO - общая для обоих треугольников

2.2) OB = OC (т. к. радиусы) ⇒

Δ AOB = Δ AOC по гипотенузе и катету ⇒ соответственные углы и стороны равны ⇒ AB = AC, что и требовалось доказать.

P. S. - на самом деле, мы сейчас доказали теорему про равенство отрезков касательных