найдите радиус окружности, описанной около прямоугольника, стороны которого равны 6 и 8

Ответ:

5.

Пошаговое объяснение:

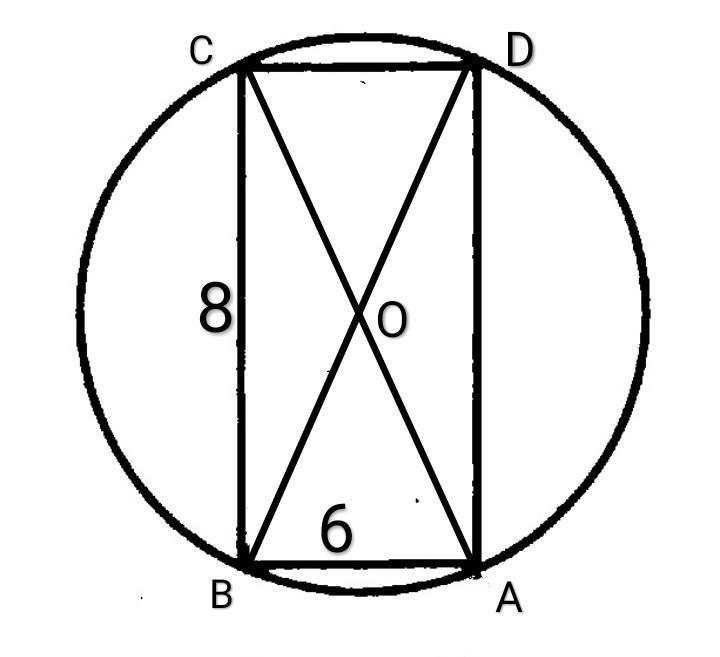
Центром окружности, описанной около прямоугольника, является точка пересечения его диагоналей. Тогда длина радиуса равна половине длины диагонали прямоугольника.

В прямоугольнике ABCD AB = 6, BC = 8.

∆ABC прямоугольный, по теореме Пифагора

АС = √(АВ² + ВС²) =√(36+64) = √100 = 10.

Тогда R = AO = 10:2 = 5.