Предмет: Математика,
автор: LenomSvamer
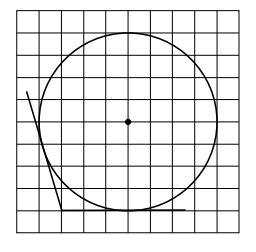
На клетчатой бумаге с размером клетки 1 x 1
изображена окружность и две касательные,
выходящие из одной точки. Найдите синус
угла между касательными к этой окружности.
Приложения:
Ответы
Автор ответа:
6
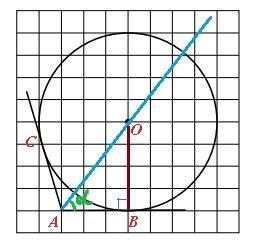
Внесем чертеж построения и обозначения.
Проведем луч АО. По свойству вписанной окружности АО - биссектриса искомого угла.
Δ АОВ - прямоугольный (ОВ⊥АВ по свойству касательной)
Обозначим ∠ОАВ = α. Задача сводится к нахождению sin (2α).
sin (2α) = 2·sin α·cos α
В Δ АОВ АВ = 3, ОВ = 4 и по теореме Пифагора АО = 5
sin α = ОВ/ОА = 4/5 = 0,8 cos α = AB/AO = 3/5 = 0,6
⇒ sin ∠CAB = 2·0,8·0,6 = 0,96
Ответ: 0,96
Приложения:
Интересные вопросы
Предмет: Русский язык,
автор: nik0903
Предмет: Русский язык,
автор: Chanterelle21
Предмет: Английский язык,
автор: Larenia
Предмет: Информатика,
автор: shmanovmisha
Предмет: Математика,
автор: skillazik