Предмет: Алгебра, автор: mejdiana0

Помогите пожалуйста! Только можно подробное объяснение!
Задание:
Постройте график функций. Определите при каких значениях k прямая y=kx не имеет с графиком общих точек.

Приложения:

Ответы

Автор ответа: nikebod313

$y = \dfrac{3|x| - 1}{|x| - 3x^{2}}$

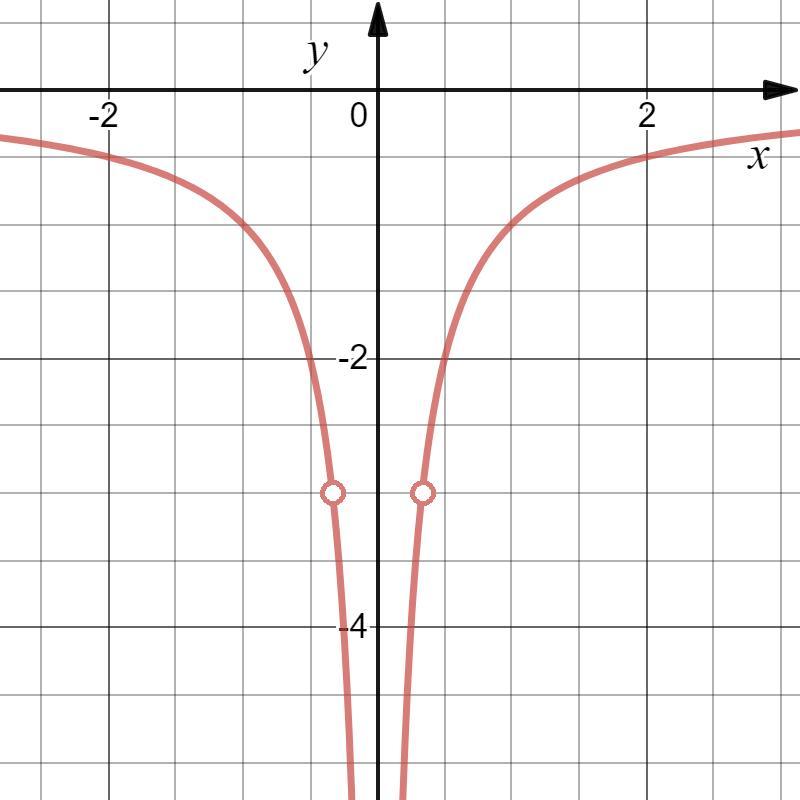
Область определения функции:

$|x| - 3x^{2} \neq 0$

$|x| \neq 3x^{2}$

$\displaystyle \left \{ {{x \neq 3x^{2} \ \ } \atop {x \neq -3x^{2}}} \right.$

$\displaystyle \left \{ {{3x^{2} - x \neq 0} \atop {3x^{2} + x \neq 0 }} \right.$

$\displaystyle \left \{ {{x(3x - 1) \neq 0} \atop {x(3x + 1) \neq 0 }} \right.$

$\left\{\begin{array}{ccc}x \neq -\dfrac{1}{3} \\x\neq 0 \ \ \ \\x \neq \dfrac{1}{3} \ \ \end{array}\right$

Применим свойство $x^{2} = |x|^{2}$ и получаем следующее:

$y = \dfrac{3|x| - 1}{|x| - 3|x|^{2}} = -\dfrac{3|x| - 1}{|x|(3|x| - 1)} = -\dfrac{1}{|x|}$

Следовательно, изобразим график функции $y = -\dfrac{1}{|x|}$ с учетом области определения (см. вложение).

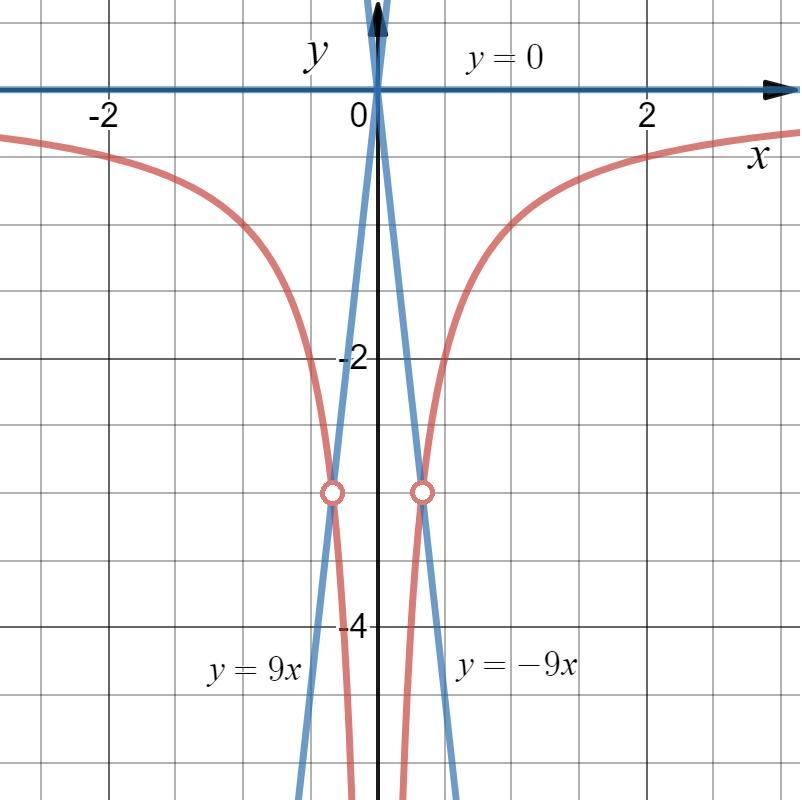
Прямая $y = kx$ — прямая пропорциональность — не будет иметь с графиком функции $y = \dfrac{3|x| - 1}{|x| - 3x^{2}}$ ни одной общей точки (см. вложение), если:

$1) \ x = -\dfrac{1}{3}; \ y = -3 \Rightarrow -3 = -\dfrac{1}{3}k \Rightarrow k = 9 \\2) \ x = \dfrac{1}{3}; \ y = -3 \Rightarrow -3 = \dfrac{1}{3}k \Rightarrow k = -9\\3) \ k = 0$