Предмет: Алгебра, автор: kostromanikita

Найдите sin^{2}\frac{x}{2} , если ctg(\frac{\pi}{2}+x)=2\sqrt{6} , x\in(\frac{\pi }{2};\pi ).

Приложения:

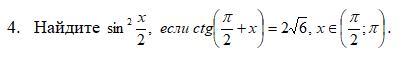
Ответы

Автор ответа: Artem112
1

По формуле приведения получим:

\mathrm{ctg}\left(\dfrac{\pi}{2}+x\right)=-\mathrm{tg}x=2\sqrt{6}

\mathrm{tg}x=-2\sqrt{6}

Выразим косинус через тангенс:

1+\mathrm{tg}^2x=\dfrac{1}{\cos^2x}

\cos^2x=\dfrac{1}{1+\mathrm{tg}^2x}

Так как косинус во второй четверти отрицателен, то:

\cos x=-\sqrt{\dfrac{1}{1+\mathrm{tg}^2x} }

Выразим искомое выражение:

\sin^2\dfrac{x}{2} =\dfrac{1-\cos x}{2} =\dfrac{1+\sqrt{\dfrac{1}{1+\mathrm{tg}^2x} }}{2}

\sin^2\dfrac{x}{2} =\dfrac{1+\sqrt{\dfrac{1}{1+(-2\sqrt{6})^2} }}{2}=\dfrac{1+\sqrt{\dfrac{1}{1+24} }}{2}=\dfrac{1+\dfrac{1}{5}}{2}=\dfrac{3}{5}

Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Русский язык, автор: olgaserichenko1

Спишите,вставляя где нужно пропущенные буквы и распределяя слова по 2 группам 1)причастия . 2)деепричастия
.............................................................
Вос(?)танавливая, вос(?)тановле..ая,опечал..вшийся,опечал..вшись,встрет..в,д..монстрируя,д..бивавшийся,встрет..вший,д..минировавший, прод..монстрировав . добившись. разв..вавшийся(флаг).пр..обл..давший.ис(?)ледовав. ком(?)ентируя. прокомм(?)нтировав
2 года назад
Предмет: Другие предметы, автор: artyom1234564
 Железнодорожный транспорт сообщение кратко как можно быстрее!
2 года назад
Предмет: Английский язык, автор: cfyd
доклад на тему мой любимый питомец на английским переводе на русском
2 года назад
Предмет: Биология, автор: fofofo1
у фасоли черная окраска семенной кожуры А доминирует над белой а.При скрещивании черносеменного растения с белосеменным все растения оказались черносеменными .Определите генотип родителей и потомства
8 лет назад
Предмет: Литература, автор: пирот2
какими чертами характера наделяет автор бабушку из Детства Максима Горького?
8 лет назад