Предмет: Математика, автор: JohnatanIve

Помогите плиз сделать это) распишите подробно, чтобы можно было разобраться. Заранее благодарен.

Приложения:

Ответы

Автор ответа: bearcab

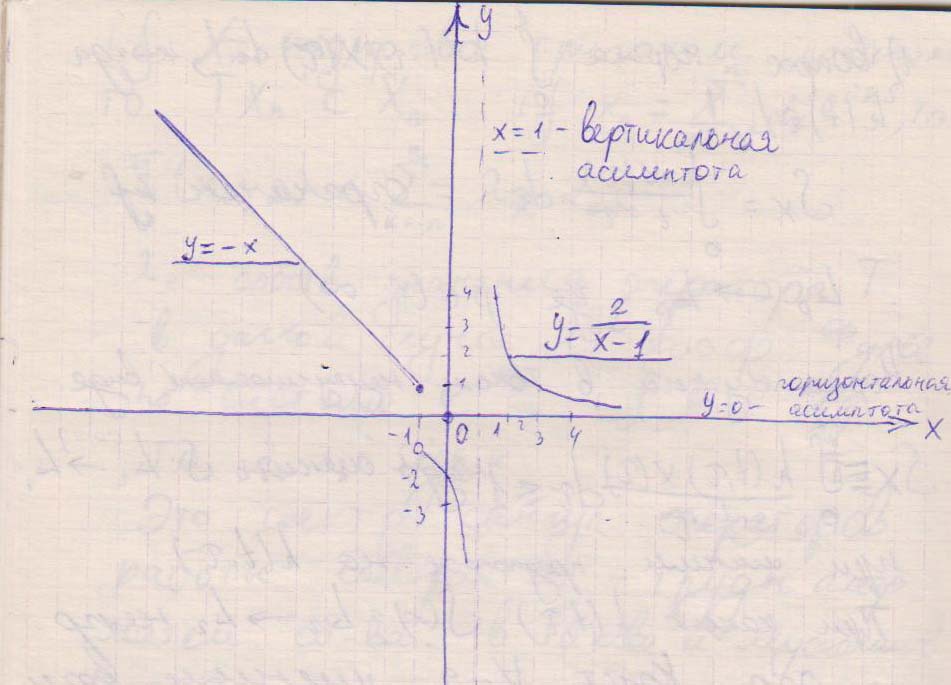
Промежутки непрерывности

$xin(-infty;,-1]cup(-1;,1)cup(1;infty)$

х=-1 - точка разрыва первого рода, так как скачок у функции конечный;

х=1 - точка разрыва второго рода, так как скачок у функции бесконечный.

График в приложении

___________________________________________________________________
Решение задачи http://znanija.com/task/3645982
Уравнение касательной в точке М(1,1) к заданной неявно функции
$x^3+3xy+y^3-5=0.$
Уравнение касательной в точке М(1,1) имеет вид

$y-y(1)=y'(1)(x-1)$
где у(1)=1, а $y'(1)$ - предстоит найти.
Возьмем производную неявной функции

$3x^2+3y+3xy'+3y^2y'=0$

Теперь поделим обе части на 3. Получим
$x^2+y+xy'+y^2y'=0$
Подставим координаты точки М в полученное выше уравнение

$1^2+1+1*y'(1)+1^2y'(1)=0$

$2+2*y'(1)=0$

Поделим обе части на 2.

$1+y'(1)=0$

$y'(1)=-1$

Теперь подставим в уравнение касательной

$y-1=-1*(x-1)$

$y-1=-x+1$

$y=-x+2$ - уравнение касательной в точке М(1; 1) к функции, заданной неявно

Ответ: у=-х+2.

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Математика, автор: darhanongar151

500. Вычислите произведен
1) -4a × 5;

2) 8b × (-3);

3) (-5c) × 2;

6 лет назад

Предмет: Русский язык, автор: darigaamre2009

Прочитай слова. Запиши одним словом, что объединяет эти слова. Составь словосочетания с этими словами *

6 лет назад

Предмет: Математика, автор: Miroslava2011sepg

6. Реши задачи. Составь и реши обратные задачи.
а) Кабачок длиной 15 см разрезали на 5 равных частей. Чему
равна длина одной части?
б) Одна третья часть урожая помидоров, собранного с огорода, сост
вила 9 кг. Сколько килограммов помидоров вырастили на огороде?

6 лет назад

Предмет: Алгебра, автор: filat

конференция по зоологии длится4 дня, в ней участвуют 60 человек, каждый выступает с одним докладом, каждый день читается по 15 докладов. Найдите вероятность того, что Григорий будет выступать со своим докладом во второй день