Предмет: Алгебра, автор: Lollpump

Очень срочно 100 баллов

Приложения:

Ответы

Автор ответа: NNNLLL54

4

$y=\dfrac{3+9x}{3x^2+x}\; \; \to \; \; \; y=\dfrac{3\, (1+3x)}{x(3x+1)}\; ,\; \; \; OOF:\; x\ne 0\; ,\; x\ne -\dfrac{1}{3}\\\\\\y=\dfrac{3}{x}\; \; ,\; \; x\ne -\dfrac{1}{3}\; ,\; x\ne 0$

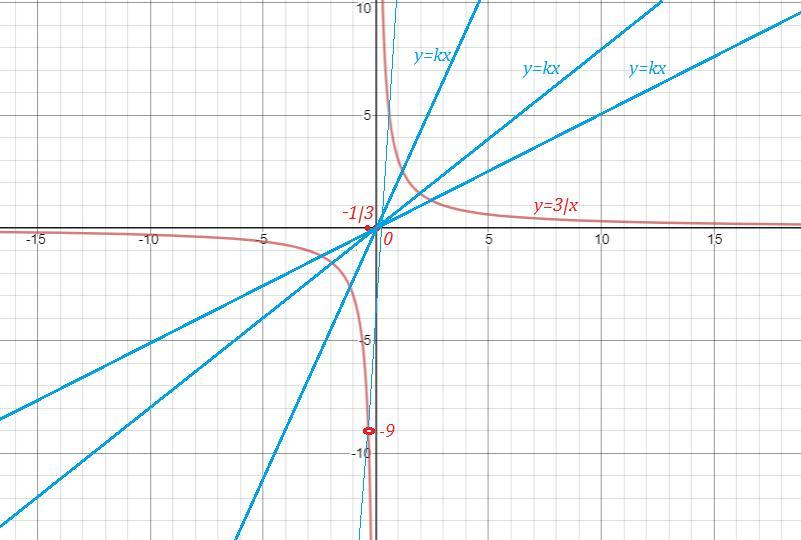
Строим гиперболу $y=\dfrac{3}{x}$ , причём выкалываем точку $(-\frac{1}{3}\, ;\, -9\, )$ .

Прямая х=0 - асимптота гиперболы , эту прямую график не пересекает

Прямая $y=kx$ имеет с данным графиком одну общую точку в случае, когда она пройдёт через выколотую точку. Подставим координаты точки в уравнение прямой и найдём уравнение этой прямой.

$y=kx\; ,\; \; x=-\frac{1}{3}\; ,\; y=-9\; \; \; \Rightarrow \; \; \; -9=-\frac{1}{3}\cdot k\; ,\; \; k=27\\\\\boxed {\; y=27\, x\; }$

Ответ: k=27 .

Приложения:

ira33388: Здравствуйте! Посмотрите мои первые вопросы - это задачи 317, 315, 295 и 286. Может вы сможете их решить, хотя бы некоторые. Пожалуйста!!

jfjc3j37: здравствуйте. пожалуйста помогите и мне.

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: Viyars

морфемный разбор прилагательного- и далёким (берегам)

2 года назад

Предмет: Русский язык, автор: poliosha2003

Какой полуостров кричит,что он самый маленький?

2 года назад

Предмет: Английский язык, автор: ispañio

Разгадайте загадку пожалуйста.
My first is the letter that comes after L,
My second is a preposition,
My third can open the door,
My whole is a funny animal.

2 года назад

Предмет: Литература, автор: КсюшаБел

Б. А. Емельянов произведения Мамины руки. Что ты можешь сказать об этой семье?

8 лет назад

Предмет: Математика, автор: алина2656

один пионер печатает 45 страниц в минуту а другой 75 страниц в минут сколько минут нужно первому пионеру чтобы напечатать 1800 страниц? сколько времени нужно для этого второму пионеру? за сколько минут будут напечатаны 1800 страниц при одновременной работе пионеров?

8 лет назад