Предмет: Математика,
автор: maziniury2014
Найти значение выражения cosx, если sinx=√3/2 и 0
Приложения:
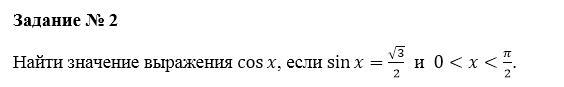
Ответы
Автор ответа:
1
sinx=√3/2
sin²x+cos²x=1
cos²x=1-(√3/2)²
cos²x=1 - 3/4
cos²x=1/4
cosx=1/2 (1 четверть).
maziniury2014:
Спасибо большое, а можете сделать этот кружочек, какие в нём значения (с четвертями)
Автор ответа:
0
В задании 2 :
в заданном диапазоне х косинус положителен. Из основного тригонометрического тождества квадрат косинуса равен 1-3/4=0,25
Значит косинус равен 0,5.
И правда : указанный диапазон - это углы прямоугольного треугольника и угол х равен 60 градусам. Синус равен корню из 3 пополам, а косинус 1/2.
В задании про 0 ничего не сказано, но замечу, что нулевого значения в этом интервале синус принимать не может (синус равен 0, если х равен пи*н, где н -любое целое)
Интересные вопросы
Предмет: Русский язык,
автор: Форевер46
Предмет: Другие предметы,
автор: verycool149
Предмет: Русский язык,
автор: margo2279
Предмет: Алгебра,
автор: seriy2003