Предмет: Алгебра, автор: rrrrtttt01

Пожалуйста помогите.................

Приложения:

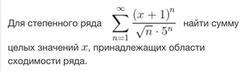
Ответы

Автор ответа: Аноним

Радиус сходимости: $R=\displaystyle \lim_{n \to \infty} \dfrac{a_n}{a_{n+1}}$ , где $a_n=\dfrac{1}{\sqrt{n}\cdot 5^n}$

$R=\displaystyle \lim_{n \to \infty} \dfrac{\dfrac{1}{\sqrt{n}\cdot 5^n}}{\dfrac{1}{\sqrt{n+1}\cdot 5^{n+1}}}= \lim_{n \to \infty} \dfrac{5\sqrt{n+1}}{\sqrt{n}}=5$

$|x+1|<5\\ \\ -5<x+1<5\\ \\ -6<x<4$

Проверим сходимость ряда на концах этого интервала

$x=-6;~~\displaystyle \sum^{\infty}_{n=1}\dfrac{(-1)^n}{\sqrt{n}\cdot 5^n}$

Этот ряд сходится по признаку Лейбница, но если взять по модулю, то по признаку Даламбера этот ряд расходится. Значит, сходится он условно. Следовательно, x = -6 — точка расходимости.

$x=4;~~\displaystyle \sum^\infty_{n=1}\dfrac{5^n}{\sqrt{n}\cdot 5^n}=\sum^\infty_{n=1}\dfrac{1}{\sqrt{n}}$