Предмет: Алгебра,
автор: DolcheGabanna
Помогите пожалуйста!!!!
Приложения:
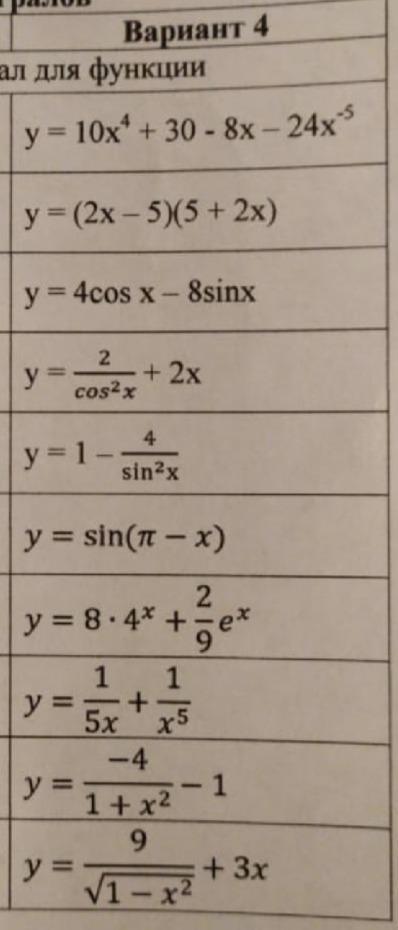
DolcheGabanna:
интеграл для функции
Ответы
Автор ответа:
1
Автор ответа:
0
1) ∫(10х⁴+30-8х-24х⁻⁵)dx=10*(x⁵/5)+30x-(8x²/2)-((24x⁻⁵⁺¹)/(-5+1))+c=
2x⁵+30x-4x²+(6/x⁴)+c;
2)упростим подынтегральную функцию (2х-5)*(5+2х)=(2х-5)*(2х+5)=4х²-25; ∫(4х²-25)dx=4x³/3-25x+c;
3) ∫(4cosx-8sinx)dx=4sinx+8cosx+c;
4) ∫((2/cos²x)+2x)dx=2tgx+(2x²/2)+c=2tgx+x²+c;
5) ∫(1-(4/(sin²x))dx=x+4ctgx+c;
6) упростим подынтегральную функцию sin(π-x)=sinx; ∫sinxdx=-cosx+c;
7) ∫(8*4ˣ+(2/9)еˣ)dx=(8*4ˣ/㏑4)+(2/9)еˣ+c;
8)∫((0.2/x)+x⁻⁵)dx=0.2㏑IxI+(x⁻⁴/(-4))+c=0.2㏑IxI-0.25/x⁴+c;
9)∫((-4/(1+x²))-1)dx=-4arctgx-x+c;
10) ∫((9/√(1-х²))+3x)dx=9arcsinx+3x²/2+c=9arcsinx+1.5x²+c.
Интересные вопросы
Предмет: Русский язык,
автор: mmyzrov
Предмет: Другие предметы,
автор: slaayer
Предмет: Английский язык,
автор: kobtsov86
Предмет: Физика,
автор: Sashulya01304
Предмет: Экономика,
автор: hiyar1Nad