Предмет: Математика,
автор: polinaka4556
Помогите пожалуйста!!!
Приложения:
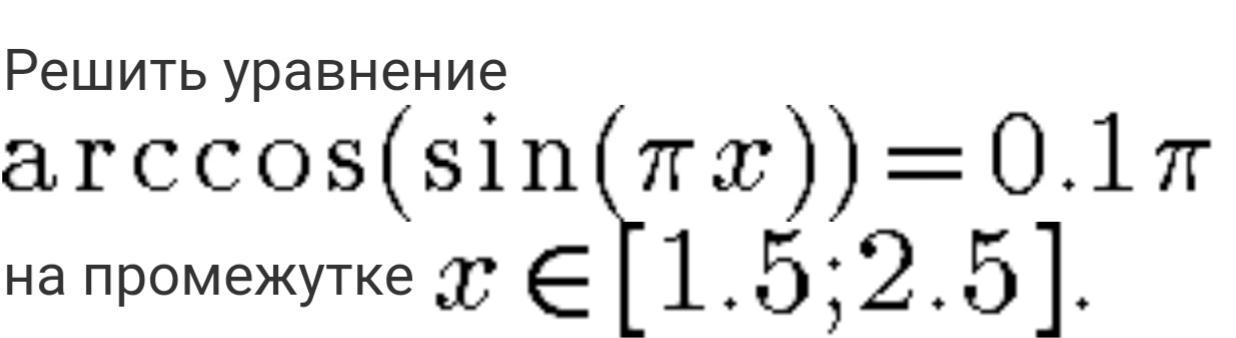
Ответы
Автор ответа:
0
y = sin(πx) - периодическая функция с периодом Т = 2π/π = 2 ⇒
sin(π(x+2)) = sinπx
Пусть sin (πx) = t ⇒ -1 ≤ t ≤ 1
откуда
arcsint = πx
Так как arcsint + arccost=π/2, то
arccost=(π/2) - arcsint=(π/2) -πх
Тогда
arccos(sinπx)=(π/2) -πх
а по условию
arccos(sinπx)=0,1π
(π/2) -πх=0,1π ⇒ х=0,5-0,1=0.4
Так как T=2
то это верно и для x=0,4+T=0,4+2=2,4
2,4∈[1,5;2,5]
О т в е т. 2, 4
Интересные вопросы
Предмет: Английский язык,
автор: fenixbaranova
Предмет: Английский язык,
автор: lerakyn
Предмет: Английский язык,
автор: Mimimi12131
Предмет: Математика,
автор: Many1211
Предмет: Математика,
автор: VictoriaLion20042004