Предмет: Математика,
автор: sproff
как было выполнено преобразование
Приложения:
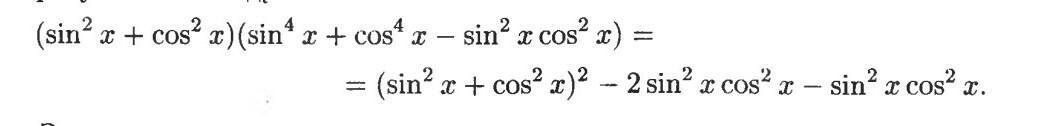
Ответы
Автор ответа:
0
Представляют сумму 4 степеней, как квадрат суммы квадратов 2 степеней без их удвоенного произведения
Приложения:

Автор ответа:
1
Первая скобка-основное тригонометрическое тождество, т.е. теорема Пифагора в тригонометрии. И эта скобка равна единице, значит, остается вторая, я ее перепишу так, чтобы Вы увидели формулу квадрата суммы двух выражений.
(sin²x)²+(cos²x)²-sin²x*cos²x
Я выделил квадрат первого выражения. это (sin²x)²; квадрат второго выражения (cos²x)², мне не хватает удвоенного произведения первого и второго либо со знаком плюс, либо со знаком минус. Лучше со знаком плюс, т.к. в скобках тогда еще раз появится единица. Итак, вычтем и добавим 2sin²x*cos²x; получим
((sin²x)²+(cos²x)²+2sin²x*cos²x- 2sin²x*cos²x)- sin²x*cos²x=
((sin²x)²+(cos²x)²+ 2sin²x*cos²x)- 2sin²x*cos²x- sin²x*cos²x=
((sin²x)+(cos²x))²-2sin²x*cos²x+sin²x*cos²x
Интересные вопросы
Предмет: Русский язык,
автор: viktorserebrya
Предмет: Русский язык,
автор: samodelkinatat
Предмет: Русский язык,
автор: goryachkina198
Предмет: Математика,
автор: Tatushka123