Предмет: Алгебра, автор: xasex8

Вычислите площадь фигуры ограниченной линиями
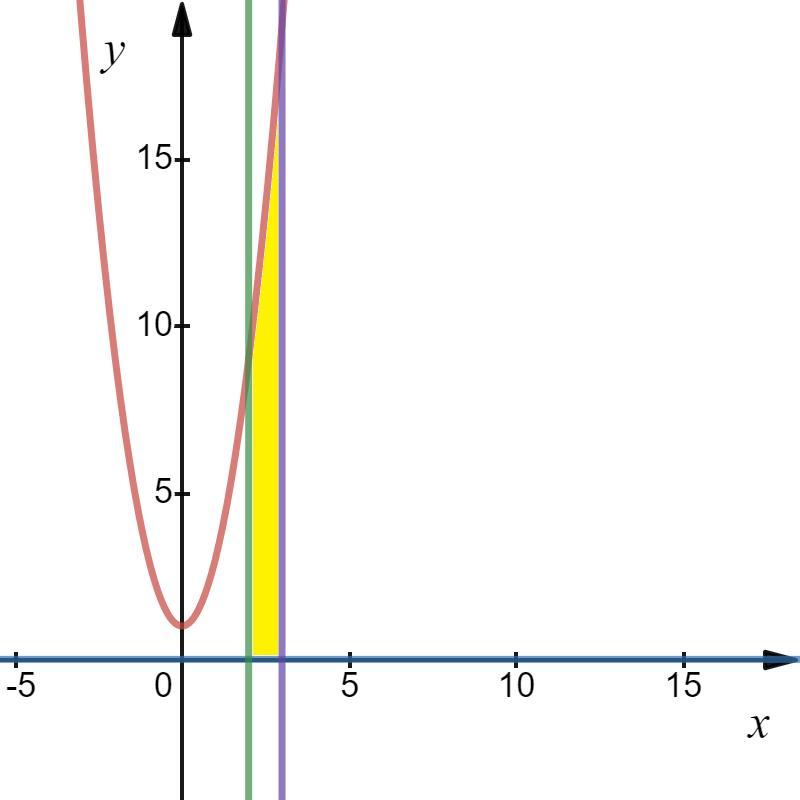
1)у=2х^2+1, у=0,х=2,х=3

Ответы

Автор ответа: nikebod313

2

Изобразим график функций $y = 2x^{2} + 1$ и $y = 0$ , а также графики уравнений $x = 2$ и $x = 3$ на координатой плоскости. Выделим область, ограниченная этими линиями, площадь которой нужно найти (см. рис.).

Площадь данной фигуры — это определенный интеграл от $x_{1} = 2$ до $x_{2}=3$ функции $y = 2x^{2} + 1$

$S = \displaystyle \int\limits_{2}^{3} (2x^{2} + 1)\, dx = \left(\dfrac{2}{3}x^{3} + x \right) \bigg |^{3}_{2} = \dfrac{2}{3} \cdot 3^{3} + 3 - \left(\dfrac{2}{3}\cdot 2^{3} + 2 \right) =$

$= \dfrac{41}{3}$ кв. ед.

Ответ: $13 \dfrac{2}{3}$ кв. ед. $\blacktriangleleft$

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: ipschein

укажите ошибки,исправьте предложение:Портрет написан известным художником,я недавно видела его на выставке.К делу была приложена характеристика заведующего.Ему приходится объяснять самые элементарные вещи.Кузнецова арестовали,и он сознался,что убил дукаревича вместе с конышевым.Усилена борьба с различными видами хищений со стороны суда,прокуратуры,милиции и хозяйственных органов.

2 года назад

Предмет: Русский язык, автор: 1anjelika1

разбор слова по составу запрокунутый оставил заплывает

2 года назад

Предмет: Українська мова, автор: 192006

какое составить предложение со словом кленовый листок на украинском языке

2 года назад

Предмет: Физика, автор: nik8896

Даны 2 планеты с массами m1 и m2 соответственно , расстояние между ними 40 км. Какое будет расстояние между планетами , если массы обеих планет увеличить в 2 раза. Силы притяжения остаётся прежней

8 лет назад

Предмет: Математика, автор: alexsandr18

помогите решить 3 любых

8 лет назад