Предмет: Алгебра,
автор: heiksteid100
Прошу помочь с нахождением производной следующих функций (100 баллов)
Приложения:
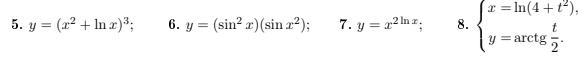
Ответы
Автор ответа:
1
heiksteid100:
Спасибо вам <3
Автор ответа:
0
5. берем производную от степенной, а потом от суммы степенной и логарифмической функций и перемножаем, т.е.
y'=((x²+lnx)³)'=3*(x²+lnx)²*(2x+(1/x))
6. y'=2sinx*cosx*sinx²+2x*sin²x*cosx²=sin2x*sinx²+2x*sin²x*cosx²
7. это логарифмическое дифференцирование. возьмем логарифмы от обеих частей. потом продифференцируем.
㏑y=㏑х^(2㏑x)
y'/y=(2㏑²x)'
y'/y=(4㏑x)/x
y'=y*(4㏑x)/x=4㏑x*x^(2㏑x-1)
8. x't=2t/(4+t²) /это икс штрих по т э/
y't=0.5*(1+t²/4)=4*0.5/(4+t²)=2/(4+t²) / это игрек штрих по тэ/
Теперь найдем игрек штрих по икс.
(2/(4+t²) ):(2t/(4+t²))=1/t
Интересные вопросы
Предмет: Русский язык,
автор: mashavedma
Предмет: Русский язык,
автор: ra72hat
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: finnk
Предмет: Математика,
автор: Zxcvbnm246